
【题目】物业公司为了改善某小区空气质量和居住环境,计划将小区内部的空地种植绿植,平时许多用户将私家车停在空地上,为了了解该小区居民对种植绿植的态度,在该小区中随机抽查了100人进行了调查,调查情况如下表:
年龄段 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 |
| 20 | 10 |
赞成人数 | 3 | 12 | 17 | 18 | 16 | 2 |
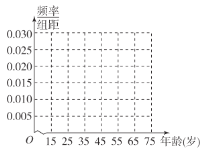
(1)求出表格中![]() 的值,并完成被调查人员年龄的频率分布图.
的值,并完成被调查人员年龄的频率分布图.
(2)若从年龄在![]() 被调查者中按照是否赞成进行分层抽样,从中抽取5人参与某项调查,然后再从这5人中随机抽取2人参加座谈会,求选出的2人中至少有1人赞成“种植绿植”的概率.
被调查者中按照是否赞成进行分层抽样,从中抽取5人参与某项调查,然后再从这5人中随机抽取2人参加座谈会,求选出的2人中至少有1人赞成“种植绿植”的概率.
【答案】(1)![]() ,见解析(2)
,见解析(2)![]()
【解析】
(1)由样本容量求出![]() 的值,填写频率分布表,即可画出频率分布直方图;
的值,填写频率分布表,即可画出频率分布直方图;
(2)由(1)知,年龄在![]() 的共有30人,其中赞成的有18人,不赞成的有12人,利用分层抽样求出抽取的5人中赞成者人数为3人,不赞成人数为2人,一一列出基本事件,根据古典概型即可求出概率.
的共有30人,其中赞成的有18人,不赞成的有12人,利用分层抽样求出抽取的5人中赞成者人数为3人,不赞成人数为2人,一一列出基本事件,根据古典概型即可求出概率.
解:(1)由题知被调查者一共100人,
所以有![]() ,
,
解得:![]() ,
,
则被调查人员年龄各组的频率为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以频率分布表如下:
年龄段 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 20 | 10 |
频率 | 0.05 | 0.15 | 0.20 | 0.30 | 0.20 | 0.10 |
频率/组距 | 0.005 | 0.015 | 0.020 | 0.030 | 0.020 | 0.010 |
所以被调查人员年龄的频率分布直方图如下图所示:

(2)由(1)知,年龄在![]() 的共有30人,其中赞成的有18人,不赞成的有12人,
的共有30人,其中赞成的有18人,不赞成的有12人,
由分层抽样赞成者应选![]() 人,记为
人,记为![]() ,
,![]() ,
,![]() ;不赞成有2人,记为
;不赞成有2人,记为![]() ,
,![]() ,
,
从中选取2人,不同的取法有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10种,
,共10种,
其中至少有1人赞成的取法有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,共9种,
,共9种,
故选出的2人中至少有1人赞成“种植绿植”的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的最大值为
的最大值为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅲ)当![]() 时,令
时,令![]() ,是否存在区间
,是否存在区间![]() .使得函数
.使得函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() 若存在,求实数
若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年起,新高考科目设置采用“![]() ”模式,普通高中学生从高一升高二时将面临着选择物理还是历史的问题,某校抽取了部分男、女学生调查选科意向,制作出如右图等高条形图,现给出下列结论:
”模式,普通高中学生从高一升高二时将面临着选择物理还是历史的问题,某校抽取了部分男、女学生调查选科意向,制作出如右图等高条形图,现给出下列结论:
①样本中的女生更倾向于选历史;
②样本中的男生更倾向于选物理;
③样本中的男生和女生数量一样多;
④样本中意向物理的学生数量多于意向历史的学生数量.
根据两幅条形图的信息,可以判断上述结论正确的有( )


A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子元件生产厂家新引进一条产品质量检测线,现对检测线进行上线的检测试验:从装有![]() 个正品和
个正品和![]() 个次品的同批次电子元件的盒子中随机抽取出
个次品的同批次电子元件的盒子中随机抽取出![]() 个,再将电子元件放回.重复
个,再将电子元件放回.重复![]() 次这样的试验,那么“取出的
次这样的试验,那么“取出的![]() 个电子元件中有
个电子元件中有![]() 个正品,
个正品,![]() 个次品”的结果恰好发生
个次品”的结果恰好发生![]() 次的概率是( )
次的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂只生产口罩、抽纸和棉签,如图是该工厂![]() 年至
年至![]() 年各产量的百分比堆积图(例如:
年各产量的百分比堆积图(例如:![]() 年该工厂口罩、抽纸、棉签产量分别占
年该工厂口罩、抽纸、棉签产量分别占![]() 、
、![]() 、
、![]() ),根据该图,以下结论一定正确的是( )
),根据该图,以下结论一定正确的是( )
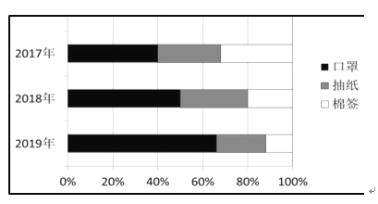
A.![]() 年该工厂的棉签产量最少
年该工厂的棉签产量最少
B.这三年中每年抽纸的产量相差不明显
C.三年累计下来产量最多的是口罩
D.口罩的产量逐年增加
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com