
已知函数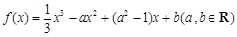
⑴若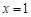 为
为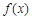 的极值点,求
的极值点,求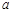 的值;
的值;
⑵若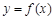 的图象在点
的图象在点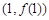 处的切线方程为
处的切线方程为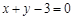 ,求
,求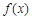 在区间
在区间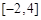 上的最大值;
上的最大值;
⑶当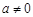 时,若
时,若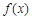 在区间
在区间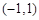 上不单调,求
上不单调,求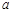 的取值范围.
的取值范围.
⑴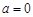 或2.⑵
或2.⑵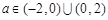 .
.
解析试题分析:⑴ ,∵
,∵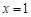 是
是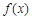 的极值点,∴
的极值点,∴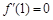 ,即
,即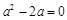 ,解得
,解得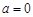 或2.
或2.
⑵∵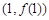 在
在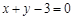 上.∴
上.∴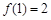 ,∵
,∵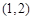 在
在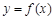 上,∴
上,∴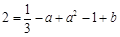 ,又
,又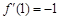 ,∴
,∴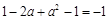 ,∴
,∴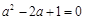 ,解得
,解得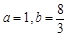 ,∴
,∴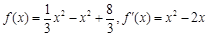 ,由
,由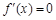 可知
可知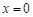 和
和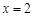 是
是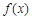 的极值点.∵
的极值点.∵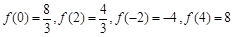 ,∴
,∴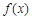 在区间
在区间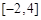 上的最大值为8.
上的最大值为8.
⑶因为函数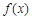 在区间
在区间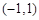 不单调,所以函数
不单调,所以函数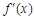 在
在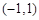 上存在零点.而
上存在零点.而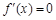 的两根为
的两根为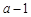 ,
,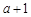 ,区间长为
,区间长为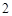 ,∴在区间
,∴在区间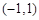 上不可能有2个零点.所以
上不可能有2个零点.所以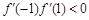 ,即
,即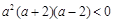 .∵
.∵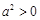 ,∴
,∴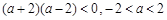 .又∵
.又∵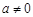 ,∴
,∴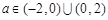 .
.
考点:本题主要考查导数计算及其几何意义,应用导数研究函数的最值。
点评:典型题,在给定区间,导数值非负,函数是增函数,导数值为非正,函数为减函数。求极值的步骤:计算导数、求驻点、讨论驻点附近导数的正负、确定极值、计算得到函数值比较大小。切线的斜率为函数在切点的导数值。(3)将条件转化成函数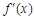 在
在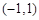 上存在零点,体现了转化与化归思想的应用。
上存在零点,体现了转化与化归思想的应用。


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com