
分析 由函数f(x)=$\frac{a^x}{{{a^x}+\sqrt{a}}}$(a>0),x1+x2=1,求出f(x1)+f(x2)=f(x1)+f(1-x1)=1,从而$f(\frac{1}{2016})+…f(\frac{2015}{2016})$=1007+f($\frac{1}{2}$),由此能求出结果.
解答 解:∵函数f(x)=$\frac{a^x}{{{a^x}+\sqrt{a}}}$(a>0),x1+x2=1,
∴f(x1)+f(x2)=f(x1)+f(1-x1)
=$\frac{{a}^{{x}_{1}}}{{a}^{{x}_{1}}+\sqrt{a}}$+$\frac{{a}^{1-{x}_{1}}}{{a}^{1-{x}_{1}}+\sqrt{a}}$
=$\frac{{a}^{{x}_{1}}}{{a}^{{x}_{1}}+\sqrt{a}}$+$\frac{a}{a+\sqrt{a}•{a}^{{x}_{1}}}$
=$\frac{{a}^{{x}_{1}}}{{a}^{{x}_{1}}+\sqrt{a}}+\frac{\sqrt{a}}{\sqrt{a}+{a}^{{x}_{1}}}$=1,
∴$f(\frac{1}{2016})+…f(\frac{2015}{2016})$=1007+f($\frac{1}{2}$)=1007+$\frac{\sqrt{a}}{\sqrt{a}+\sqrt{a}}$=$\frac{2015}{2}$.
故答案为:1,$\frac{2015}{2}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?m∈R,函数f(x)=m+$\frac{1}{{{2^x}+1}}$是偶函数 | B. | ?m∈R,函数f(x)=m+$\frac{1}{{{2^x}+1}}$是奇函数 | ||
| C. | ?m∈R,函数f(x)=m+$\frac{1}{{{2^x}+1}}$不是奇函数 | D. | ?m∈R,函数f(x)=m+$\frac{1}{{{2^x}+1}}$不是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
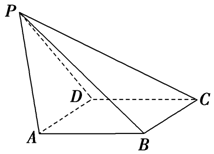 如图,已知四棱锥P-ABCD,侧面PAD是正三角形,底面ABCD是菱形,∠BAD=60°,设平面PAD∩平面PBC=l.
如图,已知四棱锥P-ABCD,侧面PAD是正三角形,底面ABCD是菱形,∠BAD=60°,设平面PAD∩平面PBC=l.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,等腰梯形ABCD中,AB∥CD,AD⊥BD,矩形ABEF所在的平面和平面ABCD相互垂直.
如图,等腰梯形ABCD中,AB∥CD,AD⊥BD,矩形ABEF所在的平面和平面ABCD相互垂直. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
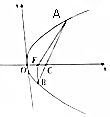 如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在x轴上,记△BCF的面积为S1,△ACF的面积为S2,则$\frac{{S}_{1}^{2}}{{S}_{2}^{2}}$等于是( )
如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在x轴上,记△BCF的面积为S1,△ACF的面积为S2,则$\frac{{S}_{1}^{2}}{{S}_{2}^{2}}$等于是( )| A. | $\frac{{|{BF}|-1}}{{|{AF}|-1}}$ | B. | $\frac{{{{|{BF}|}^2}-1}}{{{{|{AF}|}^2}-1}}$ | C. | $\frac{{|{BF}|+1}}{{|{AF}|+1}}$ | D. | $\frac{{{{|{BF}|}^2}+1}}{{{{|{AF}|}^2}+1}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com