若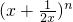 的展开式中前三项的系数依次成等差数列,则展开式中x4项的系数为________.
的展开式中前三项的系数依次成等差数列,则展开式中x4项的系数为________.
7
分析:依题意,

+


=2

×

,可求得n,由二项展开式的通项公式即可求得x
4项的系数.
解答:∵
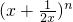
的展开式中前三项的系数依次成等差数列,
∴

+


=2

×

,
即n+

=n,解得n=8或n=1(舍).
设其二项展开式的通项为T
r+1,则T
r+1=

•x
8-r•

•x
-r=

•

•x
8-2r,
令8-2r=4得r=2.
∴展开式中x
4项的系数为
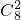
•

=28×

=7.
故答案为:7.
点评:本题考查二项式定理,通过等差数列的性质考查二项展开式的通项公式,考查分析与计算能力,属于中档题.
练习册系列答案
相关习题
科目:高中数学
来源:2011-2012学年重庆市高三第五次月考文科数学
题型:选择题
若 的展开式中前三项的系数成等差数列,则展开式中的有理项共有(
)
的展开式中前三项的系数成等差数列,则展开式中的有理项共有(
)
A.2项 B.3项 C.4项 D.5项
查看答案和解析>>
科目:高中数学
来源:2011-2012学年上海市徐汇区高三第一学期学习能力诊断卷理科数学
题型:填空题
若 的展开式中前三项的系数依次成等差数列,则展开式中
的展开式中前三项的系数依次成等差数列,则展开式中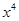 项的系数为
项的系数为
查看答案和解析>>
科目:高中数学
来源:2013年重庆市高考数学终极预测试卷(文科)(解析版)
题型:填空题
若
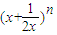
的展开式中前三项的系数依次成等差数列,则展开式中x
4项的系数为
.
查看答案和解析>>
科目:高中数学
来源:2012年上海市徐汇区高考数学一模试卷(理科)(解析版)
题型:解答题
若
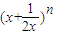
的展开式中前三项的系数依次成等差数列,则展开式中x
4项的系数为
.
查看答案和解析>>
科目:高中数学
来源:2012年上海市徐汇区高考数学一模试卷(文科)(解析版)
题型:解答题
若
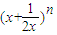
的展开式中前三项的系数依次成等差数列,则展开式中x
4项的系数为
.
查看答案和解析>>

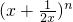 的展开式中前三项的系数依次成等差数列,则展开式中x4项的系数为________.
的展开式中前三项的系数依次成等差数列,则展开式中x4项的系数为________. 的展开式中前三项的系数成等差数列,则展开式中的有理项共有(
)
的展开式中前三项的系数成等差数列,则展开式中的有理项共有(
)