
 为半径的圆的位置关系是
为半径的圆的位置关系是  为半径的圆的位置关系,只需求得圆心到直线的距离,连接OD交CE于F,根据切线的性质,得到要求的距离即是OF,且发现四边形AEFD是矩形.再根据矩形的性质以及垂径定理和勾股定理,即可求解.
为半径的圆的位置关系,只需求得圆心到直线的距离,连接OD交CE于F,根据切线的性质,得到要求的距离即是OF,且发现四边形AEFD是矩形.再根据矩形的性质以及垂径定理和勾股定理,即可求解.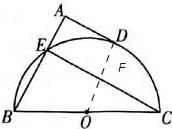 解:连接OD交CE于F,则OD⊥AD.
解:连接OD交CE于F,则OD⊥AD. =3>
=3> ,
,

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 5 |
| 2 |
| A、相离 | B、相交 | C、相切 | D、不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•江苏一模)选做题
(2012•江苏一模)选做题| 3 |
|
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
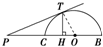
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源:2011年高三数学一轮精品复习学案:2.6 函数应用(解析版) 题型:选择题
 为半径的圆的位置关系是 ( )
为半径的圆的位置关系是 ( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com