
【题目】有一块三角形边角地,如图![]() ,
,![]() ,
,![]() ,
,![]() .(单位为百米).欲利用这块地修一个三角形形状的草坪(图中
.(单位为百米).欲利用这块地修一个三角形形状的草坪(图中![]() )供市民休闲,其中点
)供市民休闲,其中点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,沿
上,沿![]() 的三边修建休闲长廊,规划部门要求
的三边修建休闲长廊,规划部门要求![]() 的面积占
的面积占![]() 面积的一半,设
面积的一半,设![]() (百米),
(百米),![]() 的周长为
的周长为![]() (百米)
(百米)

(1)求出![]() 函数的解析式及定义域
函数的解析式及定义域
(2)求出休闲长廊总长度![]() 的取值范围,并确定当
的取值范围,并确定当![]() 取到最大值时点
取到最大值时点![]() ,
,![]() 的位置
的位置
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,用一平面去截球![]() ,所得截面面积为
,所得截面面积为![]() ,球心
,球心![]() 到截面的距离为3,
到截面的距离为3,![]() 为截面小圆圆心,
为截面小圆圆心,![]() 为截面小圆的直径.
为截面小圆的直径.
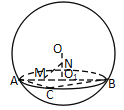
(1)计算球![]() 的表面积和体积;
的表面积和体积;
(2)若![]() 是截面小圆上一点,
是截面小圆上一点,![]() ,
,![]() 分别是线段
分别是线段![]() 和
和![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成的角(结果用反三角表示).
所成的角(结果用反三角表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某产品的销售额![]() 与广告费用
与广告费用![]() 之间的关系如下表:
之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 |
| 10 | 15 |
| 30 | 35 |
若根据表中的数据用最小二乘法求得![]() 对
对![]() 的回归直线方程为
的回归直线方程为![]() ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.产品的销售额与广告费用成正相关
B.该回归直线过点![]()
C.当广告费用为10万元时,销售额一定为74万元
D.![]() 的值是20
的值是20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将数列![]() 的前
的前![]() 项分成两部分,且两部分的项数分别是
项分成两部分,且两部分的项数分别是![]() ,若两部分和相等,则称数列
,若两部分和相等,则称数列![]() 的前
的前![]() 项的和能够进行
项的和能够进行![]() 等和分割.
等和分割.
(1)若![]() ,试写出数列
,试写出数列![]() 的前
的前![]() 项和所有等和分割;
项和所有等和分割;
(2)求证:等差数列![]() 的前
的前![]() 项的和能够进行
项的和能够进行![]() 等和分割;
等和分割;
(3)若数列![]() 的通项公式为:
的通项公式为:![]() ,且数列
,且数列![]() 的前
的前![]() 项的和能够进行等和分割,求所有满足条件的
项的和能够进行等和分割,求所有满足条件的![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将6名党员干部分配到4个贫困村驻村扶贫,每个贫困村至少分配1名党员干部,则不同的分配方案共有( )
A.2640种B.4800种C.1560种D.7200种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为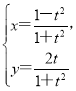 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求C的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)求C上的点到![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 m、n 是两条不同的直线,α、β、γ是三个不同的平面,下列命题中正确的是( )
A.若α⊥β , β⊥γ ,则α∥γ
B.若 ![]() ,
, ![]() , m∥n ,则α∥β
, m∥n ,则α∥β
C.若 m、n 是异面直线, ![]() , m∥β ,
, m∥β , ![]() , n∥α ,则α∥β
, n∥α ,则α∥β
D.平面α内有不共线的三点到平面 β的距离相等,则α∥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了促进某产品的销售,随机调查了该产品的月销售单价x(单位:元/件)及相应月销量y(单位:万件),对近5个月的月销售单价![]() 和月销售量
和月销售量![]() 的数据进行了统计,得到如下数表:
的数据进行了统计,得到如下数表:
月销售单价 | 8 | 8.5 | 9 | 9.5 | 10 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(1)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)该公司年底开展促销活动,当月销售单价为7元/件时,其月销售量达到14.8万件,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过0.5万件,则认为所得到的回归直线方程是理想的,试问(1)中得到的回归直线方程是否理想?
(3)根据(1)的结果,若该产品成本是5元/件,月销售单价![]() 为何值时,公司月利润的预报值最大?(注:利润=销售收入-成本).
为何值时,公司月利润的预报值最大?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中 ,
,![]()
参考数据:![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com