
【题目】给出下列五个结论:
①在△ABC中,若sinA>sinB,则必有cosA<cosB;
②在△ABC中,若a,b,c成等比数列,则角B的取值范围为 ![]() ;
;
③等比数列{an}中,若a3=2,a7=8,则a5=±4;
④等差数列{an}的前n项和为Sn , S10<0且S11=0,满足Sn≥Sk对n∈N*恒成立,则正整数k构成集合为{5,6}
⑤若关于x的不等式(a2﹣1)x2﹣(a﹣1)x﹣1<0的解集为R,则a的取值范围为 ![]() .
.
其中正确结论的序号是 . (填上所有正确结论的序号).
【答案】①②④
【解析】解:①在△abc中,sinA>sinB,根据正弦定理,根据大边对大角可得A>B,根据余弦的图象,可得cosA<cosB,所以正确;
②根据已知得:b2=ac,由余弦定理可得cosB= ![]() =
= ![]() ≥
≥ ![]() =
= ![]() ,可得B∈
,可得B∈ ![]() ,所以正确;
,所以正确;
③由 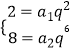 ,解得a1=1,q2=2,可得:a5=
,解得a1=1,q2=2,可得:a5= ![]() =4,所以不正确;
=4,所以不正确;
④解:∵Sn是等差数列{an}的前n项和,S10<0,且S11=0,
∴ ![]() ,即
,即 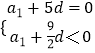 ④,
④,
∴d>0,a6=a1+5d=0,
∴a1到a5都是负数,a6是0,以后各项全是正数.
∵Sn≥Sk对n∈N+恒成立,∴k=5,或k=6.
∴正整数k构成的集合为{5,6}.故正确;
⑤解:设函数f(x)=(a2﹣1)x2﹣(a﹣1)x﹣1.由题设条件关于x的不等式(a2﹣1)x2﹣(a﹣1)x﹣1<0的解集为R.
可得对任意的x属于R.都有f(x)<0.
又当a≠1时,函数f(x)是关于x的抛物线.故抛物线必开口向下,且于x轴无交点.
故满足 ![]()
故解得﹣ ![]() <x<1.
<x<1.
当a=1时.f(x)=﹣1.成立.
综上,a的取值范围为(﹣ ![]() ,1].
,1].
故不正确.所以答案是:①②④.
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 在
在![]() 的单调区间;
的单调区间;
(Ⅱ)方程![]() 有3个不同的实根,求实数
有3个不同的实根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,若对于任意的
时,若对于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求满足条件的正整数
,求满足条件的正整数![]() 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在直线上![]() ,且与直线
,且与直线![]() 相切于点
相切于点![]()
(1)求圆C的方程;
(2)是否存在过点![]() 的直线
的直线![]() 与圆C交于
与圆C交于![]() 两点,且
两点,且![]() 的面积为
的面积为![]() (O为坐标原点),若存在,求出直线
(O为坐标原点),若存在,求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数y=f(x)是减函数,且对任意的a∈R,都有f(﹣a)+f(a)=0,若x、y满足不等式f(x2﹣2x)+f(2y﹣y2)≤0,则当1≤x≤4时,x﹣3y的最大值为( )
A.10
B.8
C.6
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了选拔优秀学生参加广州市高二级数学竞赛.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取了5次,记录如下(单位:分):
甲 83 81 79 95 92
乙 92 85 75 88 90
(1)甲乙两人分数的极差分别是多少?并用茎叶图表示这两组数据.
(2)甲乙两人这5次成绩的平均分和方差各是多少?从稳定性的角度考虑,你认为选派哪位学生参加比赛较合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱 ![]() 中,侧面
中,侧面![]() 和侧面
和侧面![]() 都是矩形,
都是矩形, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() 分别为
分别为![]() 的中点.
的中点.
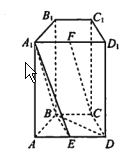
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() .
.
(3)若![]() 平面
平面![]() ,求棱
,求棱![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知美国苹果公司生产某款iPhone手机的年固定成本为40万美元,每生产1万只还需另投入16万美元.设苹果公司一年内共生产该款iPhone手机x万只并全部销售完,每万只的销售收入为R(x)万美元,且R(x)=
(1)写出年利润W(万美元)关于年产量x(万只)的函数解析式;
(2)当年产量为多少万只时,苹果公司在该款iPhone手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com