
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 利用角平分线的性质、三角形内切圆的性质、向量的运算性质即可得出.
解答 解:∵$|\overrightarrow{PA}-\overrightarrow{PB}|=|\overrightarrow{AB}|=10$,PC是∠APB角的平分线,
又满足$\overrightarrow{BI}$=$\overrightarrow{BA}$+λ($\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$+$\frac{\overrightarrow{AP}}{|\overrightarrow{AP}|}$)(λ>0),即$\overrightarrow{AI}$=λ$(\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}+\frac{\overrightarrow{AP}}{|\overrightarrow{AP}|})$,
所以I在∠BAP的角平分线上,由此得I是△ABP的内心,过I作IH⊥AB于H,I为圆心,IH为半径,作△PAB的内切圆,如图,分别切PA,PB于E、F,
∵$|\overrightarrow{PA}|-|\overrightarrow{PB}|=4$,$|\overrightarrow{PA}-\overrightarrow{PB}|=10$,$|\overrightarrow{BH}|$=$|\overrightarrow{BF}|$=$\frac{1}{2}(|\overrightarrow{PB}|+|\overrightarrow{AB}|-|\overrightarrow{PA}|)$=$\frac{1}{2}[|\overrightarrow{AB}|-(|\overrightarrow{PA}|-|\overrightarrow{PB}|)]$=3,
在直角三角形BIH中,cos∠IBH=$\frac{|\overrightarrow{BH}|}{|\overrightarrow{BI}|}$,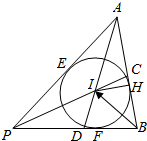
所以$\frac{{\overrightarrow{BI}•\overrightarrow{BA}}}{{|\overrightarrow{BA}|}}$=$|\overrightarrow{BI}|$cos∠IBH=$|\overrightarrow{BH}|$=3.
故选:B.
点评 本题主要考查向量运算、数量积及其几何意义、圆的切线长等,考查了数形结合方法、推理能力与计算能力,属于难题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
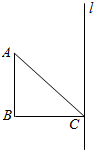 如图,三角形ABC是等腰直角三角形,∠B=90°,AB=1,直线l经过点C且与AB平行,将三角形ABC绕直线l旋转一周得到一个几何体.
如图,三角形ABC是等腰直角三角形,∠B=90°,AB=1,直线l经过点C且与AB平行,将三角形ABC绕直线l旋转一周得到一个几何体.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com