
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E,F,G分别是AB,CC1,AD的中点.
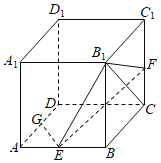
(1)求异面直线EG与B1C所成角的大小;
(2)棱CD上是否存在点T,使AT∥平面B1EF?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】已知圆C过点A(2,6),且与直线l1: x+y-10=0相切于点B(6,4).
(1)求圆C的方程;
(2)过点P(6,24)的直线l2与圆C交于M,N两点,若△CMN为直角三角形,求直线l2的斜率;
(3)在直线l3: y=x-2上是否存在一点Q,过点Q向圆C引两切线,切点为E,F, 使△QEF为正三角形,若存在,求出点Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数![]() ,其中x为自变量,a为常数.
,其中x为自变量,a为常数.
(1)若当x∈[0,2]时,函数fa(x)的最小值为﹣1,求a的值;
(2)设全集U=R,集合A={x|f3(x)≥0},B={x|fa(x)+fa(2﹣x)=f2(2)},且(UA)∩B≠![]() 中,求a的取值范围.
中,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第23届冬季奥运会于2018年2月9日至2月25日在韩国平昌举行,期间正值我市学校放寒假,寒假结束后,某校工会对全校教职工在冬季奥运会期间每天收看比赛转播的时间作了一次调查,得到如下频数分布表:

(1)若讲每天收看比赛转播时间不低于3小时的教职工定义为“体育达人”,否则定义为“非体育达人”,请根据频数分布表补全![]() 列联表:
列联表:

并判断能否有90%的把握认为该校教职工是否为“体育达人”与“性别”有关;
(2)在全校“体育达人”中按性别分层抽样抽取6名,再从这6名“体育达人”中选取2名作冬奥会知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的参数方程为
的参数方程为![]() (t为参数).
(t为参数).
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的普通方程;
的普通方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,,求点
上一点,,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数![]() 的图象向右平移一个单位,所得图象与函数
的图象向右平移一个单位,所得图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称;已知偶函数
对称;已知偶函数![]() 满足
满足![]() ,当
,当![]() 时,
时,![]() ;若函数
;若函数![]() 有五个零点,则
有五个零点,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度x/C | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,线性回归模型的残差平方和
,线性回归模型的残差平方和![]() ,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用线性回归模型,求y关于x的回归方程![]() =
=![]() x+
x+![]() (精确到0.1);
(精确到0.1);
(Ⅱ)若用非线性回归模型求得y关于x的回归方程为![]() =0.06e0.2303x,且相关指数R2=0.9522.
=0.06e0.2303x,且相关指数R2=0.9522.
( i )试与(Ⅰ)中的回归模型相比,用R2说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为

![]() =
=![]()
![]() ;相关指数R2=
;相关指数R2= .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com