
【题目】如图,在四棱锥![]() 中,
中,![]() 为等边三角形,边长为2,
为等边三角形,边长为2,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面ABCD.
平面ABCD.

(1)证明:![]() 平面PAD;
平面PAD;
(2)求平面PAD与平面PBC所成锐二面角的余弦值;
(3)棱PD上是否存在一点E,使得![]() 平面PBC?若存在,求出
平面PBC?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)棱PD上存在一点E,使得
;(3)棱PD上存在一点E,使得![]() 平面PBC,且
平面PBC,且![]() .
.
【解析】
(1)用面面垂直的性质定理证明线面垂直;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,得
,得![]() 平面
平面![]() ,以
,以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 平行于
平行于![]() 的直线为
的直线为![]() 轴,建立如图所示的空间直角坐标系,用平面的法向量的夹角求二面角;
轴,建立如图所示的空间直角坐标系,用平面的法向量的夹角求二面角;
(3)假设棱PD上存在一点E,使得![]() 平面PBC,设
平面PBC,设![]() ,由
,由![]() 与平面
与平面![]() 的法向量垂直求得
的法向量垂直求得![]() ,如果求不出,说明不存在.
,如果求不出,说明不存在.
(1)∵平面![]() 平面ABCD,
平面ABCD,![]() ,平面
,平面![]() 平面ABCD
平面ABCD![]() ,
,![]() 平面ABCD,∴
平面ABCD,∴![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由于
,由于![]() 是等边三角形,所以
是等边三角形,所以![]() ,由平面
,由平面![]() 平面ABCD,得
平面ABCD,得![]() 平面
平面![]() ,
,![]() ,
,
以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 平行于
平行于![]() 的直线为
的直线为![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,

![]() ,
,![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则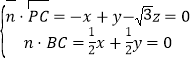 ,取
,取![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
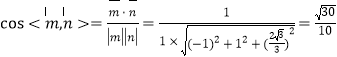 ,
,
∴平面PAD与平面PBC所成锐二面角的余弦值为![]() ;
;
(3)假设棱PD上存在一点E,使得![]() 平面PBC,设
平面PBC,设![]()
![]() ,
,
由(2)![]() ,
,![]() ,
,
![]() ,又平面
,又平面![]() 的一个法向量是
的一个法向量是![]() ,
,
∴![]() ,解得
,解得![]() ,∴
,∴![]() .
.
∴棱PD上存在一点E,使得![]() 平面PBC,且
平面PBC,且![]() .
.


科目:高中数学 来源: 题型:
【题目】某“双一流A类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率分布直方图:

(1)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前两组中抽出6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人月薪都不低于1.75万元的概率;
(2)同一组数据用该区间的中点值作代表.
(i)求这100人月薪收入的样本平均数![]() 和样本方差
和样本方差![]() ;
;
(ii)该校在某地区就业的2018届本科毕业生共50人,决定于2019国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设![]() ,月薪落在区间
,月薪落在区间![]() 左侧的每人收取400元,月薪落在区间
左侧的每人收取400元,月薪落在区间![]() 内的每人收到600元,月薪落在区间
内的每人收到600元,月薪落在区间![]() 右侧的每人收取800元.
右侧的每人收取800元.
方案二:按每人一个月薪水的3%收取;用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用?
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌布娃娃做促销活动:已知有50个布娃娃,其中一些布娃娃里面有奖品,参与者可以先在50个布娃娃中购买5个,看完5个布娃娃里面的结果再决定是否将剩下的布娃娃全部购买,设每个布娃娃有奖品的概率为![]() ,且各个布娃娃是否有奖品相互独立.
,且各个布娃娃是否有奖品相互独立.
(1)记5个布娃娃中有1个有奖品的概率为![]() ,当
,当![]() 时,
时,![]() 的最大值,求
的最大值,求![]() ;
;
(2)假如这5个布娃娃中恰有1个有奖品,以上问中的![]() 作为p的值.已知每次购买布娃娃需要2元,若有中奖,则中奖者每次可得奖金15元.以最终奖金的期望作为决策依据,是否该买下剩下所有的45个布娃娃;
作为p的值.已知每次购买布娃娃需要2元,若有中奖,则中奖者每次可得奖金15元.以最终奖金的期望作为决策依据,是否该买下剩下所有的45个布娃娃;
(3)若已知50件布娃娃中有10个布娃娃有奖品,从这堆布娃娃中任意购买5个,若抽到k个有奖品可能性最大,求k的值.(k为正整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具厂拟定生产两款新毛绒玩具样品,一款为毛绒小猪,另一款为毛绒小狗.由设计图知,生产这两款毛绒玩具均需相同材质的填充物、长毛绒、天鹅绒,且每个毛绒小猪需填充物![]() 、长毛绒
、长毛绒![]() 、天鹅绒
、天鹅绒![]() ,每个毛绒小狗需填充物
,每个毛绒小狗需填充物![]() 、长毛绒
、长毛绒![]() 、天鹅绒
、天鹅绒![]() .现有所需填充物
.现有所需填充物![]() 、长毛绒
、长毛绒![]() 、天鹅绒
、天鹅绒![]() ,若每个毛绒小猪与毛绒小狗的出厂价分别为64元、36元,则生这批毛绒玩具的最大销售额为_______元.
,若每个毛绒小猪与毛绒小狗的出厂价分别为64元、36元,则生这批毛绒玩具的最大销售额为_______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,四边形ABCD为平行四边形,
中,四边形ABCD为平行四边形,![]() 且点
且点![]() 在底面上的投影H恰为CD的中点.
在底面上的投影H恰为CD的中点.
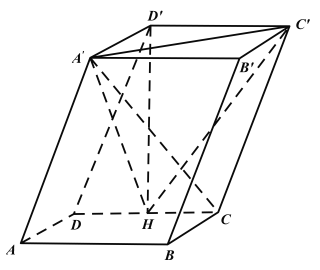
(1)棱BC上存在一点N,使得AD⊥平面![]() ,试确定点N的位置,说明理由;
,试确定点N的位置,说明理由;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com