
| A�� | �ټ������������ϵͳ�������۷ֲ���� | |
| B�� | �ٷֲ��������ϵͳ�������ۼ�������� | |
| C�� | ��ϵͳ�������ڼ�����������۷ֲ���� | |
| D�� | �ټ�����������ڷֲ��������ϵͳ���� |
���� �۲��������������ݣ������������ݵ��ص㣬�����õij���ѡ�����ټ�����������ڷֲ��������ϵͳ������
��� �⣻�۲��������������ݣ�
�ٸ���û�в��������������������������������������
�ڸ������������˲��죬����ѡ�÷ֲ���������ֲ������
�۽�����ֳɾ�������ɲ���ָ���ǽ�����ֶΣ�
�ڵ�1���ڲ��ü��������ȷ��һ����ʼ��ţ�
�ڴ˱�ŵĻ����ϼ��Ϸֶμ������������Ϊ������ţ�ϵͳ������
��ѡD��
���� �����������һ�����������ij������������õļ�������������г�ǩ������������������������ϵͳ���������У�ÿ�����屻��ȡ�Ŀ���������ȵģ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
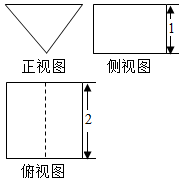 һ�������������ͼ��ͼ��ʾ������ͼΪ����ֱ�������Σ�����ͼ������ƽ�־��ε��������ö�����ı����Ϊ��������
һ�������������ͼ��ͼ��ʾ������ͼΪ����ֱ�������Σ�����ͼ������ƽ�־��ε��������ö�����ı����Ϊ��������| A�� | 2 | B�� | 4+2$\sqrt{2}$ | C�� | 4+4$\sqrt{2}$ | D�� | 6+4$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 2 | C�� | ��-2��16�� | D�� | ��2��-16�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=2cos��2x+1�� | B�� | y=2cos��2x-1�� | C�� | y=2cos2x-1 | D�� | y=2cos2x+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0��f��-1����f��5�� | B�� | f��-1����f��5����0 | C�� | f��5����f��-1����0 | D�� | f��-1����0��f��5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+2y-3=0 | B�� | x-2y+1=0 | C�� | 2x+y-3=0 | D�� | 2x-y-1=0 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com