
分析 (1)设点D(x,y)为抛物线C1上任意一点,则$|{D{C_1}}|=\sqrt{{{(x-1)}^2}+{y^2}}=\sqrt{{x^2}-2(1-p)x+1}(x≥0)$,分类讨论求p的取值范围;
(2)求出A,B的坐标,利用斜率公式,即可证明直线AB的斜率是非零常数.
解答 解:(1)由已知有C1(1,0),设点D(x,y)为抛物线C1上任意一点,则$|{D{C_1}}|=\sqrt{{{(x-1)}^2}+{y^2}}=\sqrt{{x^2}-2(1-p)x+1}(x≥0)$
令f(x)=x2-2(1-p)x+1,x∈[0,+∞),即当且仅当x=0时,f(x)有最小值1,
若0<p<1,则当x=1-p取到最小值,令1-p=0,则p=1,矛盾;
若p≥1,则当x=0取到最小值1,符合要求,
综上p≥1
(2)设直线MA的斜率为k,直线MB的斜率为-k,k≠0,
直线MA的方程为y-y0=k(x-x0),将$x=\frac{y^2}{2p}$代入整理得到ky2-2py+2py0-2pkx0=0,
则${y_A}+{y_0}=\frac{2p}{k}$,那么${y_A}=\frac{2p}{k}-{y_0}$,
又yA-y0=k(xA-x0),整理得到${x_A}=\frac{2p}{k^2}-\frac{{2{y_0}}}{k}+{x_0}$,
将其中的k换成-k,得到${x_B}=\frac{2p}{k^2}+\frac{{2{y_0}}}{k}+{x_0}$,${y_B}=-\frac{2p}{k}-{y_0}$
那么直线AB的斜率${K_{AB}}=\frac{{{y_B}-{y_A}}}{{{x_B}-{x_A}}}=\frac{{-\frac{2p}{k}-{y_0}-(\frac{2p}{k}-{y_0})}}{{\frac{2p}{k^2}+\frac{{2{y_0}}}{k}+{x_0}-(\frac{2p}{k^2}-\frac{{2{y_0}}}{k}+{x_0})}}=-\frac{p}{y_0}$
点评 本题考查直线与抛物线的性质和应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
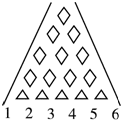 某个游戏中,一个珠子按如图所示的通道,由上至下的滑下,从最下面的六个出口出来,规定猜中者为胜,如果某人在该游戏中,猜得珠子从3号口出来,那么他取胜的概率为$\frac{5}{16}$.
某个游戏中,一个珠子按如图所示的通道,由上至下的滑下,从最下面的六个出口出来,规定猜中者为胜,如果某人在该游戏中,猜得珠子从3号口出来,那么他取胜的概率为$\frac{5}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,5} | B. | {1,2,4,5} | C. | {1,5} | D. | {2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 递增数列 | B. | 递减数列 | C. | 摆动数列 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com