
����Ŀ��ijӡˢ��Ϊ���о�ӡˢ�����鼮�ijɱ�y����λ��Ԫ����ӡˢ����x����λ��ǧ�ᣩ֮��Ĺ�ϵ����ӡ��ij���鼮ʱ������ͳ�ƣ�������ݼ��±���

�����������ݣ�������Ա�ֱ�����ס������ֲ�ͬ�Ļع�ģ�ͣ��õ��������ع鷽�̣��ף� ![]()
Ϊ����������ģ�͵����Ч���������������
��1������������±�����������ȷ��0.1����
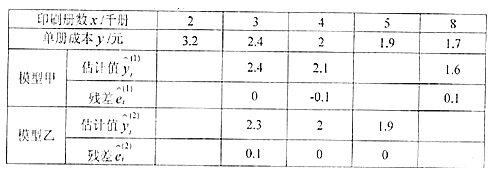
�������ֱ����ģ�ͼ���ģ���ҵIJв�ƽ����![]() ��
��![]() ����ͨ���Ƚ�
����ͨ���Ƚ�![]() ,
,![]() �Ĵ�С���ж��ĸ�ģ�����Ч������.
�Ĵ�С���ж��ĸ�ģ�����Ч������.
��2���������к��ܵ������ߵ����һ�ӭ�����ñ�ȫ������������ӡˢ���������ж���ӡˢ�������г����飬��������Ϊ8ǧ�ᣨ����Ϊ0.8����10ǧ�ᣨ����Ϊ0.2������ӡˢ����û��5Ԫ�ļ۸��鼮���۸������̣���ӡˢ������ӡˢ8ǧ�ỹ��10ǧ����ø������������1�������Ч���Ϻõ�ģ�ͼ���ӡˢ������ijɱ���
���𰸡���1��(��)������(��)ģ���ҵ����Ч�����ã���2��ӡˢ8ǧ���ӡˢ����������
�������������������1��(��)���ݹ�ʽ���㣬�����Ӧ����(��) �Ƚ��в�ƽ������С��ԽСԽ������ģ���ҵ����Ч�����ã���2���ֱ����ӡˢ8ǧ����10ǧ������������ӡˢ8ǧ�ᣬ��ӡˢ������Ϊ![]() (Ԫ)��������ӡˢ10ǧ�ᣬ��ÿ���ɱ�Ϊ
(Ԫ)��������ӡˢ10ǧ�ᣬ��ÿ���ɱ�Ϊ![]() ����������ֵΪ
����������ֵΪ![]() ���������Ϊ
���������Ϊ![]() ������ӡˢ8ǧ���������.
������ӡˢ8ǧ���������.
����������⣺(��) (��) �����㣬�ɵ��±���
ӡˢ���� | 2 | 3 | 4 | 5 | 8 | |
����ɱ� | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
ģ�ͼ� | ����ֵ | 3.1 | 2.4 | 2.1 | 1.9 | 1.6 |
�в� | 0.1 | 0 | -0.1 | 0 | 0.1 | |
ģ���� | ����ֵ | 3.2 | 2.3 | 2 | 1.9 | 1.7 |
�в� | 0 | 0.1 | 0 | 0 | 0 | |
(��) ![]() ��
�� ![]() ��
��
![]() ����ģ���ҵ����Ч�����ã�
����ģ���ҵ����Ч�����ã�
(��) ������ӡˢ8ǧ�ᣬ��ӡˢ������Ϊ![]() (Ԫ) ��
(Ԫ) ��
������ӡˢ10ǧ�ᣬ��(��)��֪��������ӡˢ�ɱ�Ϊ![]() (Ԫ)��
(Ԫ)��
��ӡˢ�ܳɱ�Ϊ![]() (Ԫ) ��
(Ԫ) ��
����������Ϊ![]() (ǧ��)��ӡˢ������Ϊ
(ǧ��)��ӡˢ������Ϊ![]() (Ԫ)����
(Ԫ)����
| 8 | 10 |
| 0.8 | 0.2 |
![]() ��
��
��![]() ��
��
��ӡˢ8ǧ���ӡˢ����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() ���뾶Ϊ
���뾶Ϊ![]() ��Բ
��Բ![]() ��
��![]() ���У�Բ��
���У�Բ��![]() ��
��![]() ��������ֱ��
��������ֱ��![]() ���Ϸ���
���Ϸ���
������Բ![]() �ı����̣�
�ı����̣�
������![]() ��ֱ����Բ
��ֱ����Բ![]() ����
����![]() ���㣨
���㣨![]() ��
��![]() ���Ϸ���������
���Ϸ���������![]() �����������Ƿ���ڵ�
�����������Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ��ƽ��
��ƽ��![]() �������ڣ��������
�������ڣ��������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�����������������˶�Աÿ�������÷ֵľ�Ҷͼ����������˱����÷ֵ���λ��֮���� 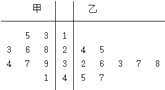
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��������һ�������ͼס��ҡ�����4����ɵ���Ⱥ�������Ⱥ�������ÿ�η�����ĸ���Ϊ1����С���Լ�������������ס��ҡ���3��ÿ�����ú���ĸ�����ͬ��
������С����2�κ�������ǡ��1�����ú���ĸ��ʣ�
������С����3�κ�������е�1��2�Σ�ÿ�η�5Ԫ�ĺ������3�η�10Ԫ�ĺ���������������к����Ǯ��֮��ΪX����X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ռ��ı���ABCD�������Խ��ߵij�AC=6��BD=8��AC��BD���ɵĽ�Ϊ30o �� E��F��G��H�ֱ���AB��BC��CD��DA���е㣬���ı���EFGH�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԭ��Ķ�ֱ��l��ԲC1��x2+y2��6x+5=0�ཻ�ڲ�ͬ������A��B��
��1����ԲC1��Բ�����ꣻ
��2�����߶�AB ���е�M�Ĺ켣C�ķ��̣�
��3���Ƿ����ʵ�� k��ʹ��ֱ��L��y=k��x��4�������� Cֻ��һ�����㣿�����ڣ����k��ȡֵ��Χ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ��������30�ˣ�������90�ˣ�������60�ˣ�Ϊ�˵������ǵ����彡��״�������÷ֲ�����ķ����������м��ȡһ������Ϊ36����������Ӧ��ȡ�����˵������ǣ� ��
A.5
B.6
C.7
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ![]() ��Բ
��Բ![]() ��ֱ������
��ֱ������![]() ��Բ
��Բ![]() �ϣ�����
�ϣ�����![]() ���ڵ�ƽ�洹ֱ��Բ
���ڵ�ƽ�洹ֱ��Բ![]() ���ڵ�ƽ�棬
���ڵ�ƽ�棬 ![]() ��
��
��1��֤����ƽ��![]() ��ƽ��
��ƽ��![]() ��
��
��2��������![]() ��������ʱ�����
��������ʱ�����![]() ��ƽ��
��ƽ��![]() �ľ��룮
�ľ��룮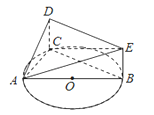
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]()
��1���� ![]() ʱ���ⲻ��ʽf��x����x+10��
ʱ���ⲻ��ʽf��x����x+10��
��2������x�IJ���ʽf��x����a��R�Ϻ��������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com