练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知球面上有S，A，B，C四点，且SA⊥平面ABC，∠ABC=90°，SC=2．则该球的表面积为
     
    ．
    考点：球的体积和表面积
    专题：计算题,空间位置关系与距离
    分析：求得球的直径为SC=2，可得球的半径，即可求出球的表面积．
    解答： 解：∵球面上有S，A，B，C四点，且SA⊥平面ABC，∠ABC=90°，SC=2，
    ∴球的直径为SC=2，
    ∴球的半径为1，
    ∴球的表面积为4π．
    故答案为：4π．
    点评：本题考查球的表面积，考查学生的计算能力，比较基础．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知数列{an}满足：a1=a，an+1=
    1
    2
    an2-an    +2，其中n∈N*．
    （Ⅰ）是否存在实数a使得{an}为等差数列，若存在，求出a的值，若不存在，请说明理由；
    （Ⅱ）当a=4时，证明：
    1
    a1
    +
    1
    a2
    +…+
    1
    an
    ＜
    1
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=loga（x+1），a＞1，对于定义域内的x1，x2有0＜x1＜x2＜1，给出下列结论：
    ①（x2-x1）[f（x2）-f（x1）]＜0；
    ②x2f（x1）＜x1f（x2）；
    ③f（x2）-f（x1）＞x1-x2；
    ④
    f(x1)+f(x2)
    2
    ＜f（
    x1+x2
    2
    ）．
    其中正确结论的序号是（　　）
    A、①②B、①③C、②④D、③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设a是实数，且
    1+i
    i
    +
    ai
    1-i
    （i是虚数单位）是实数，则a=（　　）
    A、2
    B、
    3
    2
    C、1
    D、
    1
    2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

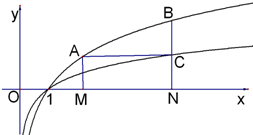    如图，过函数f（x）=logcx（c＞1）的图象上的两点A，B作x轴的垂线，垂足分别为M（a，0），N（b，0）（b＞a＞1），线段BN与函数g（x）=logmx，（m＞c＞1）的图象交于点C，且AC与x轴平行．
    （1）当a=2，b=4，c=3时，求实数m的值；
    （2）当b=a2时，求
    m
    b
    -
    2c
    a
    的最小值；
    （3）已知h（x）=ax，φ（x）=bx，若x1，x2为区间（a，b）内任意两个变量，且x1＜x2，求证：h[f（x2）]＜φ[f（x1）]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若方程
    x2
    3-m
    +
    y2
    m-1
    =1表示椭圆，则实数m的取值范围
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在圆x2+y2-2x-6y=0内，过点E（0，1）的最长弦和最短弦分别是AC和BD，则四边形ABCD的面积为（　　）
    A、5
    		2
    B、20
    		2
    C、15
    		2
    D、10
    		2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    第三赛季甲、乙两名运动员每场比赛得分的茎叶图如图所示，则下列说法中正确的是（　　）
    A、甲、乙两人单场得分的最高分都是9分
    B、甲、乙两人单场得分的中位数相同
    C、甲运动员的得分更集中，发挥更稳定
    D、乙运动员的得分更集中，发挥更稳定．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

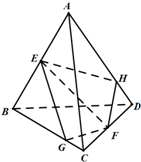    如图，在四面体ABCD中，E，F分别为AB，CD的中点，过EF任作一个平面α分别与直线BC，AD相交于点G，H，有下列三个结论，其中正确的个数是（　　）
    ①对于任意的平面α，都有直线GF，EH，BD相交于同一点；
    ②存在一个平面α0，使得点G在线段BC上，点H在线段AD的延长
    线上；
    ③对于任意的平面α，它把三棱锥的体积分成相等的两部分．
    A、0B、1C、2D、3

    查看答案和解析>>

    同步练习册答案