Question

【题目】已知函数.

（Ⅰ）求证：1是函数的极值点;

（Ⅱ）设是函数的导函数，求证： .

Answer 1

【答案】（Ⅰ）证明见解析；（Ⅱ）证明见解析.

【解析】试题分析：（Ⅰ）求函数的导数，分析导数在1两侧的符号，判定1是极值点；（Ⅱ）求出的导数，找到，列表求出函数的最小值即可证明.

试题解析：（Ⅰ）证明：

证法1： 的定义域为

由得

， .

当时， ， ，故在上单调递增；

当时， ， ，故在上单调递减；

所以1是函数的极值点.

证法2：（根据极值的定义直接证明）

的定义域为

，

当时， ，即；

当时， ，即；

根据极值的定义，1是的极值点.

（Ⅱ）由题意可知，

证法1： ，

令，

，故在上单调递增. 又，又在上连续，

使得，即，

.（*）

随x的变化情况如下：

	↘	极小值	↗

………………10分

.

由（*）式得，代入上式得

.

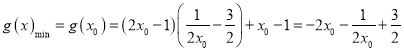令，

，故在上单调递减.

，又， .

即 .

证法2： ，

令，

随x的变化情况如下：

	↘	极小值	↗

，即，当且仅当时取到等号.

，令得.

随x的变化情况如下：

	↘	极小值	↗

，即，当且仅当时取到等号. .即.