
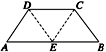
如图所示,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合,求形成的三棱锥的外接球的体积.
外接球体积为![]() ×OA3=
×OA3=![]() ·
·![]() ·
·![]() =
=![]()
由已知条件知,平面图形中AE=EB=BC=CD=DA=DE=EC=1
∴折叠后得到一个正四面体. 2分
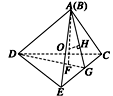
方法一 作AF⊥平面DEC,垂足为F,F即为△DEC的中心.
取EC的中点G,连接DG、AG,
过球心O作OH⊥平面AEC.
则垂足H为△AEC的中心. 4分
∴外接球半径可利用△OHA∽△GFA求得.
 ∵AG=
∵AG=![]() ,AF=
,AF=![]() =
=![]() , 6分
, 6分
在△AFG和△AHO中,根据三角形相似可知,
AH=![]() .∴OA=
.∴OA=![]() =
=![]() =
=![]() . 10分
. 10分
∴外接球体积为![]() ×OA3=
×OA3=![]() ·
·![]() ·
·![]() =
=![]() . 14分
. 14分
方法二 如图所示,把正四面体放在正方体中.显然,正四面体
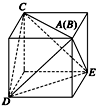 的外接球就是正方体的外接球. 6分
的外接球就是正方体的外接球. 6分
∵正四面体的棱长为1,
∴正方体的棱长为![]() ,∴外接球直径2R=
,∴外接球直径2R=![]() ·
·![]() , 10分
, 10分
∴R=![]() ,∴体积为
,∴体积为![]() ·
·![]() =
=![]() . 12分
. 12分
∴该三棱锥外接球的体积为![]() . 14分
. 14分


科目:高中数学 来源: 题型:
 如图所示,在等腰梯形ABCD中,AB∥DC,AB=3,DC=1,tanB=2,点M是梯形ABCD内(含边界)的一个动点,则
如图所示,在等腰梯形ABCD中,AB∥DC,AB=3,DC=1,tanB=2,点M是梯形ABCD内(含边界)的一个动点,则| AD |
| AM |
查看答案和解析>>
科目:高中数学 来源:2012年云南省昆明市高三复习教学质量检测数学试卷(理科)(解析版) 题型:填空题
 的最大值是 .
的最大值是 .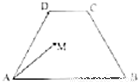
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三第一学期八校联考理科数学 题型:解答题
(本题满分15分) 如图所示,在等腰梯形 中,
中, ,
, ,
, 为
为 中点.将
中点.将 沿
沿 折起至
折起至 ,使得平面
,使得平面 平面
平面 ,
, 分别为
分别为 的中点.
的中点.
(Ⅰ) 求证: 面
面 ;
;
(Ⅱ) 求二面角 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
如图所示,在等腰梯形![]() 中,
中,![]()
![]() 为
为![]() 边上一点,且
边上一点,且![]() 将
将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ⊥平面
⊥平面![]() .
.
(1)求证:![]() ⊥平面
⊥平面![]() ;
;
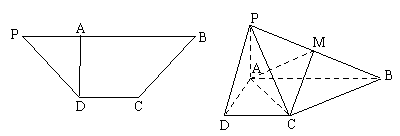 (2)若
(2)若![]() 是侧棱
是侧棱![]() 中点,求截面
中点,求截面![]() 把几何体分成的两部分的体积之比。
把几何体分成的两部分的体积之比。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com