
ĄūĖâÄŋĄŋÄģĘýŅ§ÐĄŨéĩ――øÐÐÉįŧáĘĩžųĩũēéĢŽÁË―âöÎöÎÍ°Ũ°ËŪūÓŠēŋÔÚΊČįšÎķĻžÛ·ĒģîĄĢ―øŌŧē―ĩũŅÐÁË―âĩ―ČįÏÂÐÅÏĒĢšļÃūÓŠēŋÃŋĖėĩÄ·ŋŨâĄĒČËÔąđĪŨĘĩČđĖķĻģÉąūΊ200ÔŠĢŽÃŋÍ°ËŪĩÄ―øžÛĘĮ5ÔŠĢŽÏúĘÛĩĨžÛÓëČÕūųÏúĘÛÁŋĩÄđØÏĩČįÏÂąíĢš
ÏúĘÛĩĨžÛ/ÔŠ | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
ČÕūųÏúĘÛÁŋ/Í° | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
ļųūÝŌÔÉÏÐÅÏĒĢŽÄãČÏΊļÃūÓŠēŋķĻžÛΊķāÉŲēÅÄÜŧņĩÃŨîīóĀûČóĢŋĢĻ ĢĐ
A.ÃŋÍ°8.5ÔŠB.ÃŋÍ°9.5ÔŠC.ÃŋÍ°10.5ÔŠD.ÃŋÍ°11.5ÔŠ
Ąūīð°ļĄŋD
Ąū―âÎöĄŋ
ÍĻđýąíļņŋÉÖŠÏúĘÛĩĨžÛÃŋÔöžÓ1ÔŠĄĒČÕūųÏúĘÛÁŋžõÉŲ40Í°ĢŽ―øķøÁÐģöąíīïĘ―ĢŽĀûÓÃķþīΚŊĘýĩÄžōĩĨÐÔÖĘžīĩÃ―áÂÛĢŪ
ÍĻđýąíļņŋÉÖŠÏúĘÛĩĨžÛÃŋÔöžÓ1ÔŠĄĒČÕūųÏúĘÛÁŋžõÉŲ40Í°ĢŽÉčÃŋÍ°ËŪĩÄžÛļņΊĢĻ6+xĢĐÔŠĢĻ0ĢžxĢž13ĢĐĢŽ
đŦËūČÕĀûČóyÔŠĢŽÔōyĢ―ĢĻ6+xĐ5ĢĐĢĻ480Đ40xĢĐĐ200Ģ―Đ40x2+440x+280ĢĻ0ĢžxĢž13ĢĐĢŽ
ĄßĐ40Ģž0ĢŽĄāĩąxĢ―![]() Ģ―5.5ĘąšŊĘýyÓÐŨîīóÖĩĢŽ
Ģ―5.5ĘąšŊĘýyÓÐŨîīóÖĩĢŽ
ŌōīËĢŽÃŋÍ°ËŪĩÄžÛļņΊ6+5.5=11.5ÔŠĢŽđŦËūČÕĀûČóŨîīóĢŽ
đĘŅĄĢšD


 ÐĄŅ§ÆÚÄĐģåīĖ100·ÖÏĩÁÐīð°ļ
ÐĄŅ§ÆÚÄĐģåīĖ100·ÖÏĩÁÐīð°ļ ÆÚÄĐļīÏ°žėēâÏĩÁÐīð°ļ
ÆÚÄĐļīÏ°žėēâÏĩÁÐīð°ļ ģŽÄÜŅ§ĩäĩĨÔŠÆÚÖÐÆÚÄĐŨĻĖâģåīĖ100·ÖÏĩÁÐīð°ļ
ģŽÄÜŅ§ĩäĩĨÔŠÆÚÖÐÆÚÄĐŨĻĖâģåīĖ100·ÖÏĩÁÐīð°ļ ŧÆļÔ360ķČķĻÖÆÃÜūíÏĩÁÐīð°ļ
ŧÆļÔ360ķČķĻÖÆÃÜūíÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠÖąÏß![]() ūđýÍÖÔē
ūđýÍÖÔē![]() ĢĻ
ĢĻ![]() ĢĐĩÄŨóķĨĩã
ĢĐĩÄŨóķĨĩã![]() šÍ
šÍ
ÉÏķĨĩã![]() ĢŪÍÖÔē
ĢŪÍÖÔē![]() ĩÄÓŌķĨĩãΊ
ĩÄÓŌķĨĩãΊ![]() ĢŽĩã
ĢŽĩã![]() ĘĮÍÖÔē
ĘĮÍÖÔē![]() ÉÏÎŧÓÚ
ÉÏÎŧÓÚ![]() ÖáÉÏ·―ĩÄķŊĩãĢŽÖąÏß
ÖáÉÏ·―ĩÄķŊĩãĢŽÖąÏß![]() ĄĒ
ĄĒ![]() ÓëÖąÏß
ÓëÖąÏß![]()
![]() ·Öąð―ŧÓÚ
·Öąð―ŧÓÚ![]() ĄĒ
ĄĒ![]() Á―ĩãĢŪ
Á―ĩãĢŪ
ĢĻĒņĢĐĮóÍÖÔē![]() ĩÄąęŨž·―ģĖĢŧ
ĩÄąęŨž·―ģĖĢŧ
ĢĻĒōĢĐĮóÏßķÎ![]() ģĪķČĩÄŨîÐĄÖĩĢŧ
ģĪķČĩÄŨîÐĄÖĩĢŧ
ĢĻĒóĢĐĩąÏßķÎ![]() ĩÄģĪķČŨîÐĄĘąĢŽÍÖÔē
ĩÄģĪķČŨîÐĄĘąĢŽÍÖÔē![]() ÉÏĘĮ·ņīæÔÚÕâŅųĩÄĩã
ÉÏĘĮ·ņīæÔÚÕâŅųĩÄĩã![]() ĢŽĘđĩÃ
ĢŽĘđĩÃ![]() ĩÄÃæŧýΊ
ĩÄÃæŧýΊ![]() ĢŋČôīæÔÚĢŽČ·ķĻĩã
ĢŋČôīæÔÚĢŽČ·ķĻĩã![]() ĩÄļöĘýĢŧČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉĢŪ
ĩÄļöĘýĢŧČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÉč![]() ĄĒ
ĄĒ![]() ĄĒ
ĄĒ![]() ĘĮČýĖõēŧÍŽĩÄÖąÏßĢŽ
ĘĮČýĖõēŧÍŽĩÄÖąÏßĢŽ![]() ĄĒ
ĄĒ![]() ĄĒ
ĄĒ![]() ĘĮČýļöēŧÍŽĩÄÆ―ÃæĢŽļøģöÏÂÁÐËÄļöÃüĖâĢš
ĘĮČýļöēŧÍŽĩÄÆ―ÃæĢŽļøģöÏÂÁÐËÄļöÃüĖâĢš
ĒŲČô![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽÔō
ĢŽÔō![]() Ģŧ
Ģŧ
ĒÚČô![]() ĢŽ
ĢŽ![]() ĢŽÔō
ĢŽÔō![]() Ģŧ
Ģŧ
ĒÛČô![]() ĢŽ
ĢŽ![]() ĘĮÁ―ĖõŌėÃæÖąÏßĢŽ
ĘĮÁ―ĖõŌėÃæÖąÏßĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĮŌ
ĮŌ![]() ĢŽÔō
ĢŽÔō![]() Ģŧ
Ģŧ
ĒÜČô![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽÔō
ĢŽÔō![]() .
.
ÆäÖÐÕýČ·ÃüĖâĩÄÐōšÅĘĮĢĻ ĢĐ
A.ĒŲĒÛB.ĒŲĒÜC.ĒÚĒÛD.ĒÚĒÜ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠķĻŌåÔÚ![]() ÉÏĩÄŋÉĩžšŊĘý
ÉÏĩÄŋÉĩžšŊĘý![]() ĢŽķÔÓÚČÎŌâĘĩĘý
ĢŽķÔÓÚČÎŌâĘĩĘý![]() ķžÓÐ
ķžÓÐ![]() ģÉÁĒĢŽĮŌĩą
ģÉÁĒĢŽĮŌĩą![]() ĘąĢŽķžÓÐ
ĘąĢŽķžÓÐ![]() ģÉÁĒĢŽČô
ģÉÁĒĢŽČô![]() ĢŽÔōĘĩĘý
ĢŽÔōĘĩĘý![]() ĩÄČĄÖĩ·ķΧΊĢĻ ĢĐ
ĩÄČĄÖĩ·ķΧΊĢĻ ĢĐ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠÍÖÔē![]() ĩÄŌŧļö―đĩãÓëÅŨÎïÏß
ĩÄŌŧļö―đĩãÓëÅŨÎïÏß![]() ĩÄ―đĩãÖØšÏĢŽĮŌÍÖÔē
ĩÄ―đĩãÖØšÏĢŽĮŌÍÖÔē![]() ĩÄĀëÐÄÂĘΊ
ĩÄĀëÐÄÂĘΊ![]() .
.
ĢĻ1ĢĐĮóÍÖÔē![]() ĩÄąęŨž·―ģĖĢŧ
ĩÄąęŨž·―ģĖĢŧ
ĢĻ2ĢĐÖąÏß![]() ―ŧÍÖÔē
―ŧÍÖÔē![]() ÓÚ
ÓÚ![]() ĄĒ
ĄĒ![]() Á―ĩãĢŽÏßķÎ
Á―ĩãĢŽÏßķÎ![]() ĩÄÖÐĩãΊ
ĩÄÖÐĩãΊ![]() ĢŽÖąÏß
ĢŽÖąÏß![]() ĘĮÏßķÎ
ĘĮÏßķÎ![]() ĩÄīđÖąÆ―·ÖÏßĢŽĮóÖĪĢšÖąÏß
ĩÄīđÖąÆ―·ÖÏßĢŽĮóÖĪĢšÖąÏß![]() đýķĻĩãĢŽēĒĮóģöļÃķĻĩãĩÄŨøąęĢŪ
đýķĻĩãĢŽēĒĮóģöļÃķĻĩãĩÄŨøąęĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠšŊĘý![]() .
.
ĢĻ1ĢĐĮó![]() ĩÄÍžÏņÔÚ
ĩÄÍžÏņÔÚ![]() īĶĩÄĮÐÏß·―ģĖĢŧ
īĶĩÄĮÐÏß·―ģĖĢŧ
ĢĻ2ĢĐĮóšŊĘý![]() ĩÄžŦīóÖĩĢŧ
ĩÄžŦīóÖĩĢŧ
ĢĻ3ĢĐČô![]() ķÔ
ķÔ![]() šãģÉÁĒĢŽĮóĘĩĘýaĩÄČĄÖĩ·ķΧ.
šãģÉÁĒĢŽĮóĘĩĘýaĩÄČĄÖĩ·ķΧ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠšŊĘý![]() .
.
ĢĻ1ĢĐČô![]() ĘĮķĻŌåÓōÉÏĩÄÔöšŊĘýĢŽĮó
ĘĮķĻŌåÓōÉÏĩÄÔöšŊĘýĢŽĮó![]() ĩÄČĄÖĩ·ķΧĢŧ
ĩÄČĄÖĩ·ķΧĢŧ
ĢĻ2ĢĐÉč![]() ĢŽ
ĢŽ![]() ·ÖąðΊ
·ÖąðΊ![]() ĩÄžŦīóÖĩšÍžŦÐĄÖĩĢŽČô
ĩÄžŦīóÖĩšÍžŦÐĄÖĩĢŽČô![]() ĢŽĮó
ĢŽĮó![]() ĩÄČĄÖĩ·ķΧ.
ĩÄČĄÖĩ·ķΧ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚČýĀâÖų![]() ÖÐĢŽ
ÖÐĢŽ![]() ĄĒ
ĄĒ![]() ·ÖąðĘĮ
·ÖąðĘĮ![]() ĄĒ
ĄĒ![]() ĩÄÖÐĩã.
ĩÄÖÐĩã.
ĢĻ1ĢĐÉčĀâ![]() ĩÄÖÐĩãΊ
ĩÄÖÐĩãΊ![]() ĢŽÖĪÃũĢš
ĢŽÖĪÃũĢš![]() Æ―Ãæ
Æ―Ãæ![]() Ģŧ
Ģŧ
ĢĻ2ĢĐČô![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽĮŌÆ―Ãæ
ĢŽĮŌÆ―Ãæ![]() Æ―Ãæ
Æ―Ãæ![]() ĢŽĮóČýĀâÖų
ĢŽĮóČýĀâÖų![]() ĩÄļß.
ĩÄļß.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
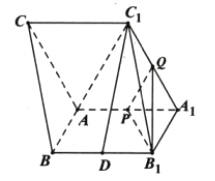
ĄūĖâÄŋĄŋŌŅÖŠAĄĒBΊÍÖÔē![]() ĢĻ
ĢĻ![]() ĢĐšÍËŦĮúÏß
ĢĐšÍËŦĮúÏß![]() ĩÄđŦđēķĨĩãĢŽPĄĒQ·ÖąðΊËŦĮúÏßšÍÍÖÔēÉÏēŧÍŽÓÚAĄĒBĩÄķŊĩãĢŽĮŌ
ĩÄđŦđēķĨĩãĢŽPĄĒQ·ÖąðΊËŦĮúÏßšÍÍÖÔēÉÏēŧÍŽÓÚAĄĒBĩÄķŊĩãĢŽĮŌ![]() ĢĻ
ĢĻ![]() ĢŽ
ĢŽ![]() ĢĐĢŽÉčAPĄĒBPĄĒAQĄĒBQĩÄÐąÂĘ·ÖąðΊ
ĢĐĢŽÉčAPĄĒBPĄĒAQĄĒBQĩÄÐąÂĘ·ÖąðΊ![]() ĄĒ
ĄĒ![]() ĄĒ
ĄĒ![]() ĄĒ
ĄĒ![]() .
.
ĢĻ1ĢĐČô![]() ĢŽĮó
ĢŽĮó![]() ĩÄÖĩĢĻÓÃaĄĒbĩÄīúĘýĘ―ąíĘūĢĐĢŧ
ĩÄÖĩĢĻÓÃaĄĒbĩÄīúĘýĘ―ąíĘūĢĐĢŧ
ĢĻ2ĢĐĮóÖĪĢš![]() Ģŧ
Ģŧ
ĢĻ3ĢĐÉč![]() ĄĒ
ĄĒ![]() ·ÖąðΊÍÖÔēšÍËŦĮúÏßĩÄÓŌ―đĩãĢŽČô
·ÖąðΊÍÖÔēšÍËŦĮúÏßĩÄÓŌ―đĩãĢŽČô![]() ĢŽĮó
ĢŽĮó![]() ĩÄÖĩĢŪ
ĩÄÖĩĢŪ
ēéŋīīð°ļšÍ―âÎö>>
°ŲķČÖÂÐÅ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com