
【题目】已知![]() 为定义在实数集
为定义在实数集![]() 上的函数,把方程
上的函数,把方程![]() 称为函数
称为函数![]() 的特征方程,特征方程的两个实根
的特征方程,特征方程的两个实根![]() 、
、![]() (
(![]() ),称为
),称为![]() 的特征根.
的特征根.
(1)讨论函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)已知![]() 为给定实数,求
为给定实数,求![]() 的表达式;
的表达式;
(3)把函数![]() ,
,![]() 的最大值记作
的最大值记作![]() ,最小值记作
,最小值记作![]() ,研究函数
,研究函数![]() ,
,![]() 的单调性,令
的单调性,令![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,上顶点为
,上顶点为![]() ,
,![]() 为坐标原点,过
为坐标原点,过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() .
.
(1)若直线![]() 垂直于
垂直于![]() 轴,求
轴,求![]() 的值;
的值;
(2)若![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则椭圆
,则椭圆![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 关于直线
关于直线![]() 成轴对称?如果存在,求出点
成轴对称?如果存在,求出点![]() 的坐标;如果不存在,请说明理由;
的坐标;如果不存在,请说明理由;
(3)设直线![]() :
:![]() 上总存在点
上总存在点![]() 满足
满足![]() ,当
,当![]() 的取值最小时,求直线
的取值最小时,求直线![]() 的倾斜角
的倾斜角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在距离为
,若存在距离为![]() 的两条直线
的两条直线![]() 和
和![]() ,使得对任意
,使得对任意![]() 都有
都有![]() 恒成立,则称函数
恒成立,则称函数![]() 有一个宽度为
有一个宽度为![]() 的通道.给出下列函数:
的通道.给出下列函数:
①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]() .
.
其中在区间![]() 上有一个通道宽度为
上有一个通道宽度为![]() 的函数是__________(写出所有正确的序号).
的函数是__________(写出所有正确的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2016-2018年文科数学全国Ⅱ卷中各模块所占分值百分比大致如图所示:

给出下列结论:
①选修1-1所占分值比选修1-2小;
②必修分值总和大于选修分值总和;
③必修1分值大致为15分;
④选修1-1的分值约占全部分值的![]() .
.
其中正确的是( )
A. ①②B. ①②③C. ②③④D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华为手机作为华为公司三大核心业务之一,2018年的销售量跃居全球第二名,某机构随机选取了100名华为手机的顾客进行调查,并将这![]() 人的手机价格按照
人的手机价格按照![]() ,
,![]() ,…
,…![]() 分成
分成![]() 组,制成如图所示的频率分布直方图,其中
组,制成如图所示的频率分布直方图,其中![]() 是
是![]() 的
的![]() 倍.
倍.

(1)求![]() ,
,![]() 的值;
的值;
(2)求这![]() 名顾客手机价格的平均数(同一组中的数据用该组区间的中间值作代表);
名顾客手机价格的平均数(同一组中的数据用该组区间的中间值作代表);
(3)利用分层抽样的方式从手机价格在![]() 和
和![]() 的顾客中选取
的顾客中选取![]() 人,并从这
人,并从这![]() 人中随机抽取
人中随机抽取![]() 人进行回访,求抽取的
人进行回访,求抽取的![]() 人手机价格在不同区间的概率.
人手机价格在不同区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 | 不喜爱打篮球 | 合 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05[ | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.072 | 2.70 | 3.841 | 5.024 | 6.635 | 7.879 | 10.82 |
(参考公式: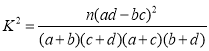 ,其中
,其中![]() )
)![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com