
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴正半轴有公共点,求
轴正半轴有公共点,求![]() 的取值范围;
的取值范围;
(2)求证:![]() 时,
时,![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)求得f(x)的导数,可得切线斜率和切点,以及切线方程,可令y=0,求得横坐标x,由题意可得x>0,解不等式可得所求范围;
(2)求得f′(x)=![]() ﹣ex+a.设g(x)=f′(x)=
﹣ex+a.设g(x)=f′(x)=![]() ﹣ex+a.判断g(x)递减,由函数零点存在定理可得g(x)存在零点x0,
﹣ex+a.判断g(x)递减,由函数零点存在定理可得g(x)存在零点x0,
求得f(x)≤f(x0),求得a,结合分析法和不等式的性质、函数的单调性,即可得证.
解:(1)函数f(x)=lnx﹣ex+a的导数为f′(x)=![]() ﹣ex+a.
﹣ex+a.
曲线f(x)在点(1,f(1))处的切线斜率为1﹣e1+a,
切点为(1,﹣e1+a),可得切线方程为y+e1+a=(1﹣e1+a)(x﹣1),
可令y=0可得x=![]() ,由题意可得
,由题意可得![]() >0,
>0,
可得e1+a<1,解得a<﹣1;
(2)证明:f′(x)=![]() ﹣ex+a.设g(x)=f′(x)=
﹣ex+a.设g(x)=f′(x)=![]() ﹣ex+a.
﹣ex+a.
可得g′(x)=﹣(![]() +ex+a),当x>0时,g′(x)<0,g(x)递减;
+ex+a),当x>0时,g′(x)<0,g(x)递减;
由a>1﹣![]() ,ex+a>ex.若ex>
,ex+a>ex.若ex>![]() ,g(x)<
,g(x)<![]() ﹣ex<0,
﹣ex<0,
当0<x<1时,ex+a<e1+a.若e1+a<![]() ,即x<e﹣1﹣a,
,即x<e﹣1﹣a,
故当0<x<e﹣1﹣a时,g(x)>0,即g(x)=f′(x)有零点x0,
当0<x<x0时,f′(x)>0,f(x)递增;当x>x0时,f′(x)<0,f(x)递减,
可得f(x)≤f(x0),
又f(x0)=lnx0﹣ex0+a,又ex0+a=![]() ,
,
可得f(x0)=lnx0﹣![]() ,在x0>0递增,
,在x0>0递增,
又a=ln![]() ﹣x0=﹣(lnx0+x0),
﹣x0=﹣(lnx0+x0),
a>1﹣![]() ﹣(lnx0+x0)>1﹣
﹣(lnx0+x0)>1﹣![]() =﹣(ln
=﹣(ln![]() +
+![]() ),
),
所以lnx0+x0<ln![]() +
+![]() ,由于lnx0+x0递增,
,由于lnx0+x0递增,
可得0<x0<![]() ,故f(x)≤f(x0)<f(
,故f(x)≤f(x0)<f(![]() )=﹣1﹣e.
)=﹣1﹣e.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】在![]() 中国北京世界园艺博览会期间,某工厂生产
中国北京世界园艺博览会期间,某工厂生产![]() 、
、![]() 、
、![]() 三种纪念品,每一种纪念品均有精品型和普通型两种,某一天产量如下表:(单位:个)
三种纪念品,每一种纪念品均有精品型和普通型两种,某一天产量如下表:(单位:个)
纪念品 | 纪念品 | 纪念品 | |
精品型 |
|
|
|
普通型 |
|
|
|
现采用分层抽样的方法在这一天生产的纪念品中抽取![]() 个,其中
个,其中![]() 种纪念品有
种纪念品有![]() 个.
个.
(1)求![]() 的值;
的值;
()从![]() 种精品型纪念品中抽取
种精品型纪念品中抽取![]() 个,其某种指标的数据分别如下:
个,其某种指标的数据分别如下:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,把这
,把这![]() 个数据看作一个总体,其均值为
个数据看作一个总体,其均值为![]() ,方差为
,方差为![]() ,求
,求![]() 的值;
的值;
(3)用分层抽样的方法在![]() 种纪念品中抽取一个容量为
种纪念品中抽取一个容量为![]() 的样木,从样本中任取
的样木,从样本中任取![]() 个纪念品,求至少有
个纪念品,求至少有![]() 个精品型纪念品的概率.
个精品型纪念品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC-A1B1C1中,AB=AA1=![]() ,AC=2,∠BAC=∠A1AC=45°,∠BAA1=60°,F为棱AC的中点,E在棱BC上,且BE=2EC.
,AC=2,∠BAC=∠A1AC=45°,∠BAA1=60°,F为棱AC的中点,E在棱BC上,且BE=2EC.
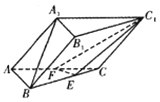
(Ⅰ)求证:A1B∥平面EFC1;
(Ⅱ)求三棱柱ABC-A1B1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】越接近高考学生焦虑程度越强,四个高三学生中大约有一个有焦虑症,经有关机构调查,得出距离高考周数与焦虑程度对应的正常值变化情况如下表周数
周数x | 6 | 5 | 4 | 3 | 2 | 1. |
正常值y | 55 | 63 | 72 | 80 | 90 | 99 |
其中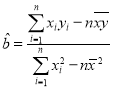 ,
,![]() ,
,![]() ,
,![]()
(1)作出散点图;
(2)根据上表数据用最小二乘法求出y关于x的线性回方程![]() (精确到0.01)
(精确到0.01)
(3)根据经验观测值为正常值的0.85~1.06为正常,若1.06~1.12为轻度焦虑,1.12~1.20为中度焦虑,1.20及以上为重度焦虑。若为中度焦虑及以上,则要进行心理疏导。若一个学生在距高考第二周时观测值为103,则该学生是否需要进行心理疏导?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品均需要![]() ,
,![]() 两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
甲 | 乙 | 原料限额 | |
| 3 | 2 | 10 |
| 1 | 2 | 6 |
A. 10万元B. 12万元C. 13万元D. 14万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间中不同直线m、n和不同平面α、β,下面四个结论:
①若m、n互为异面直线,m∥α,n∥α,m∥β,n∥β,则α∥β;
②若m⊥n,m⊥α,n∥β,则α⊥β;
③若n⊥α,m∥α,则n⊥m;
④若α⊥β,m⊥α,n∥m,则n∥β.
其中正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com