
【题目】某超市计划销售某种食品,现邀甲、乙两个商家进场试销5天.两个商家提供的返利方案如下:甲商家每天固定返利60元,且每卖出一件食品商家再返利2元;乙商家无固定返利,卖出30件以内(含30件)的食品,每件食品商家返利4元,超出30件的部分每件返利6元.经统计,两个商家的试销情况茎叶图如下:
甲 | 乙 | |||||||
9 | 8 | 9 | 2 | 8 | 8 | |||
2 | 2 | 3 | 2 | 1 | 1 | |||
(1)现从甲商家试销的5天中抽取两天,求这两天的销售量都小于30的概率;
(2)超市拟在甲、乙两个商家中选择一家长期销售,如果仅从日平均返利额的角度考虑,请利用所学的统计学知识为超市作出选择,并说明理由.
【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)先根据枚举法确定5天中抽取两天的基本事件总数,再从中确定两天的销售量都小于30的基本事件数,最后根据古典概型概率公式求概率,(2)先根据平均数计算公式求甲、乙,再根据大小确定选择.
试题解析:(1)记“抽取的两天销售量都小于30”为事件A,
则5天中抽取两天的情况有:(29,28),(29,29),(29,32),(29,32),(28,29),(28,32),(28,32),(29,32),(29,32),(32,32)共10种;
两天的销售量都小于30的情况有:(29,28),(29,29),(28,29)共3种.
所以P(A)= ![]() .
.
(2)依题意,
甲商家的日平均销售量为:
![]() .
.
所以甲商家的日平均返利额为:60+30×2=120元.
乙商家的日平均返利额为:
![]() (28×4+28×4+30×4+2×6+30×4+1×6+30×4+1×6)=121.6元.
(28×4+28×4+30×4+2×6+30×4+1×6+30×4+1×6)=121.6元.
因为121.6元>120元,
所以推荐该超市选择乙商家长期销售.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】图1,平行四边形![]() 中,
中, ![]() ,
, ![]() ,现将
,现将![]() 沿
沿![]() 折起,得到三棱锥
折起,得到三棱锥![]() (如图2),且
(如图2),且![]() ,点
,点![]() 为侧棱
为侧棱![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)在![]() 的角平分线上是否存在点
的角平分线上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(2,2,2),B(2,0,0),C(0,2,-2).
(1)写出直线BC的一个方向向量;
(2)设平面α经过点A,且BC是α的法向量,M(x,y,z)是平面α内的任意一点,试写出x,y,z满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在给出的下列命题中,正确的是( )
A.设![]() 是同一平面上的四个点,若
是同一平面上的四个点,若![]() ,则点
,则点![]() 必共线
必共线
B.若向量![]() 是平面
是平面![]() 上的两个向量,则平面
上的两个向量,则平面![]() 上的任一向量
上的任一向量![]() 都可以表示为
都可以表示为![]() ,且表示方法是唯一的
,且表示方法是唯一的
C.已知平面向量![]() 满足
满足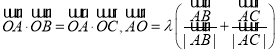 则
则![]() 为等腰三角形
为等腰三角形
D.已知平面向量![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 是等边三角形
是等边三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
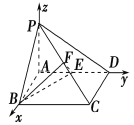
【题目】如图,在四棱锥PABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,BC=2![]() ,E,F分别是AD,PC的中点.
,E,F分别是AD,PC的中点.
(1)证明:PC⊥平面BEF;
(2)求平面BEF与平面BAP夹角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆系方程![]() :
: ![]() (
(![]() ,
, ![]() ),
), ![]() 是椭圆
是椭圆![]() 的焦点,
的焦点, ![]() 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)![]() 为椭圆
为椭圆![]() 上任意一点,过
上任意一点,过![]() 且与椭圆
且与椭圆![]() 相切的直线
相切的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,求证:
,求证: ![]() 的面积为定值,并求出这个定值.
的面积为定值,并求出这个定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的各棱长均相等,
的各棱长均相等, ![]() 底面
底面![]() ,E,F分别为棱
,E,F分别为棱![]() 的中点.
的中点.
(1)过![]() 作平面α,使得直线BE//平面α,若平面α与直线
作平面α,使得直线BE//平面α,若平面α与直线![]() 交于点H,指出点H所在的位置,并说明理由;
交于点H,指出点H所在的位置,并说明理由;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com