
【题目】(14分)关于x的不等式ax2+(a﹣2)x﹣2≥0(a∈R)
(1)已知不等式的解集为(﹣∞,﹣1]∪[2,+∞),求a的值;
(2)解关于x的不等式ax2+(a﹣2)x﹣2≥0.
【答案】(1)![]() (2)当a=0时,不等式的解集为{x|x≤﹣1},当a>0时,不等式的解集为{x|x≥
(2)当a=0时,不等式的解集为{x|x≤﹣1},当a>0时,不等式的解集为{x|x≥![]() 或x≤﹣1},当﹣2<a<0时,不等式的解集为{x|
或x≤﹣1},当﹣2<a<0时,不等式的解集为{x|![]() ≤x≤﹣1},当a=﹣2时,不等式的解集为{x|x=﹣1},当a<﹣2时,不等式的解集为{x|﹣1≤x≤
≤x≤﹣1},当a=﹣2时,不等式的解集为{x|x=﹣1},当a<﹣2时,不等式的解集为{x|﹣1≤x≤![]() }.
}.
【解析】试题分析:(1)且该不等式的解集为(﹣∞,﹣1]∪[2,+∞),∴a>0;又不等式对应方程的两个实数根为﹣1和2,从而可求出![]() 的值;(2)分四种情况讨论
的值;(2)分四种情况讨论![]() 的取值,分别根据一元二次不等式的解法求出对应不等式的解集即可.
的取值,分别根据一元二次不等式的解法求出对应不等式的解集即可.
试题解析:(1)∵关于x的不等式ax2+(a﹣2)x﹣2≥0可变形为
(ax﹣2)(x+1)≥0,
且该不等式的解集为(﹣∞,﹣1]∪[2,+∞),
∴a>0;
又不等式对应方程的两个实数根为﹣1和2;
∴![]() =2,解得a=1;
=2,解得a=1;
(2)①a=0时,不等式可化为﹣2x﹣2≥0,它的解集为{x|x≤﹣1};
②a≠0时,不等式可化为(ax﹣2)(x+1)≥0,
当a>0时,原不等式化为(x﹣![]() )(x+1)≥0,
)(x+1)≥0,
它对应的方程的两个实数根为![]() 和﹣1,且
和﹣1,且![]() >﹣1,
>﹣1,
∴不等式的解集为{x|x≥![]() 或x≤﹣1};
或x≤﹣1};
当a<0时,不等式化为(x﹣![]() )(x+1)≤0,
)(x+1)≤0,
不等式对应方程的两个实数根为![]() 和﹣1,
和﹣1,
在﹣2<a<0时,![]() <﹣1,
<﹣1,
∴不等式的解集为{x|![]() ≤x≤﹣1};
≤x≤﹣1};
在a=﹣2时,![]() =﹣1,不等式的解集为{x|x=﹣1};
=﹣1,不等式的解集为{x|x=﹣1};
在a<﹣2时,![]() >﹣1,不等式的解集为{x|﹣1≤x≤
>﹣1,不等式的解集为{x|﹣1≤x≤![]() }.
}.
综上,a=0时,不等式的解集为{x|x≤﹣1},
a>0时,不等式的解集为{x|x≥![]() 或x≤﹣1},
或x≤﹣1},
﹣2<a<0时,不等式的解集为{x|![]() ≤x≤﹣1},
≤x≤﹣1},
a=﹣2时,不等式的解集为{x|x=﹣1},
a<﹣2时,不等式的解集为{x|﹣1≤x≤![]() }
}


科目:高中数学 来源: 题型:
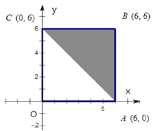
【题目】如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界)。
(Ⅰ)向区域A随机抛掷一粒黄豆,求黄豆落在区域B的概率;
(Ⅱ)若x,y分别表示甲、乙两人各掷一次骰子所得的点数,求点(x,y)落在区域B的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1= ![]() an+t,a1=
an+t,a1= ![]() (t为常数,且t≠
(t为常数,且t≠ ![]() ).
).
(1)证明:{an﹣2t}为等比数列;
(2)当t=﹣ ![]() 时,求数列{an}的前几项和最大?
时,求数列{an}的前几项和最大?
(3)当t=0时,设cn=4an+1,数列{cn}的前n项和为Tn , 若不等式 ![]() ≥2n﹣7对任意的n∈N*恒成立,求实数k的取值范围.
≥2n﹣7对任意的n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(14分)一根直木棍长为6m,现将其锯为2段.
(1)若两段木棍的长度均为正整数,求恰有一段长度为2m的概率;
(2)求锯成的两段木棍的长度均大于2m的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程![]() ,其左焦点、上顶点和左顶点分别为
,其左焦点、上顶点和左顶点分别为![]() ,
, ![]() ,
, ![]() ,坐标原点为
,坐标原点为![]() ,且线段
,且线段![]() ,
, ![]() ,
, ![]() 的长度成等差数列.
的长度成等差数列.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若过点![]() 的一条直线
的一条直线![]() 交椭圆于点
交椭圆于点![]() ,
, ![]() ,交
,交![]() 轴于点
轴于点![]() ,使得线段
,使得线段![]() 被点
被点![]() ,
, ![]() 三等分,求直线
三等分,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是平行四边行,
是平行四边行, ![]() 平面
平面![]() ,
, ![]() //
// ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)证明: ![]() //平面
//平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(4)求二面角![]() 的平面角的正切值.
的平面角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com