
分析 (1)由题及抛物线的定义知,轨迹M是以定点(1,0)为焦点,直线x=-1为准线的抛物线,由此能求出动圆圆心的轨迹M的方程.
(2)由点差法求出${k_{CD}}=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{4}{{{y_1}+{y_2}}}$,设直线PC的斜率为k,则直线PD的斜率为-k,从而lPC:y-2=k(x-1),则由$\left\{{\begin{array}{l}{{y^2}=4x}\\{y-2=k({x-1})}\end{array}}\right.⇒k{y^2}-4y-4k+8=0$,从而得到${y_1}=\frac{4}{k}-2$,同理得${y_2}=-\frac{4}{k}-2$,由此能求出直线CD的斜率为定值-1.
解答 解:(1)由题及抛物线的定义知,轨迹M是以定点(1,0)为焦点,直线x=-1为准线的抛物线,
∴$\frac{ϕ}{2}=1$,∴ϕ=2,
即动圆圆心的轨迹M的方程为:y2=4x…(4分)
(2)由题知$\left\{{\begin{array}{l}{y_1^2=4{x_1}\;\;\;\;①}\\{y_2^2=4{x_2}②}\end{array}}\right.$,
由①-②得(y1+y2)(y1-y2)=4(x1-x2),
∴${k_{CD}}=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{4}{{{y_1}+{y_2}}}$…(6分)
设直线PC的斜率为k,则直线PD的斜率为-k,
∴lPC:y-2=k(x-1),则由$\left\{{\begin{array}{l}{{y^2}=4x}\\{y-2=k({x-1})}\end{array}}\right.⇒k{y^2}-4y-4k+8=0$,
∴${y_1}+2=\frac{4}{k}$,∴${y_1}=\frac{4}{k}-2$,
同理得${y_2}=-\frac{4}{k}-2$…(10分)
∴${k_{CD}}=\frac{4}{{{y_1}+{y_2}}}=\frac{4}{{({\frac{4}{k}-2})+({-\frac{4}{k}-2})}}=-1$,
即直线CD的斜率为定值-1.…(12分)
点评 本题考查动圆圆心的轨迹方程的求法,考查直线的斜率是否为定值的判断与求法,考查圆的方程、直线与圆的位置关系,考查推理论证能力、运算求解能力,考查转化化归思想、数形结合思想,是中档题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| A | 85 | 80 | 85 | 60 | 90 |
| B | 70 | 90 | 95 | 70 | 75 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
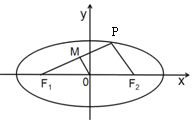 已知P为椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上任意一点,F1,F2为左、右焦点,M为PF1中点.如图所示:若|OM|+$\frac{1}{2}$|PF1|=2,离心率e=$\frac{\sqrt{3}}{2}$.
已知P为椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上任意一点,F1,F2为左、右焦点,M为PF1中点.如图所示:若|OM|+$\frac{1}{2}$|PF1|=2,离心率e=$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2+\sqrt{2}}}{2}$ | B. | $\frac{{2-\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com