【题目】下列说法错误的是
A. 对分类变量X与Y，随机变量K2的观测值k越大，则判断“X与Y有关系”的把握程度越小
B. 在回归直线方程
=0.2x+0.8中，当解释变量x每增加1个单位时，预报变量
平均增加0.2个单位
C. 两个随机变量的线性相关性越强，则相关系数的绝对值就越接近于1
D. 回归直线过样本点的中心（
， 
）
科目：高中数学 来源： 题型：
【题目】为研究某种图书每册的成本费
（元）与印刷数
（千册）的关系，收集了一些数据并作了初步处理，得到了下面的散点图及一些统计量的值.
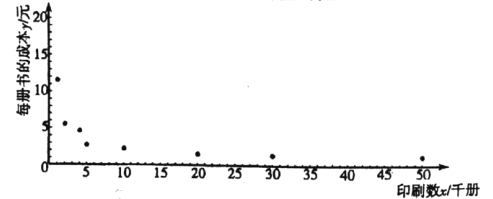
表中
， 
.
（1）根据散点图判断： 
与
哪一个更适宜作为每册成本费
（元）与印刷数
（千册）的回归方程类型？（只要求给出判断，不必说明理由）
（2）根据（1）的判断结果及表中数据，建立
关于
的回归方程（回归系数的结果精确到0.01）；
（3）若每册书定价为10元，则至少应该印刷多少千册才能使销售利润不低于78840元？（假设能够全部售出，结果精确到1）
（附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为
， 
）
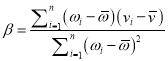查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知一工厂生产了某种产品700件，该工厂对这些产品进行了安全和环保这两个性能的质量检测。工厂决定利用随机数表法从中抽取100件产品进行抽样检测，现将700件产品按001，002，…,700进行编号；
（1）如果从第8行第4列的数开始向右读，请你依次写出最先检测的3件产品的编号；
（下面摘取了随机数表的第7～9行）
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
（2）抽取的100件产品的安全性能和环保性能的质量检测结果如下表：
检测结果分为优等、合格、不合格三个等级，横向和纵向分别表示安全性能和环保性能。若在该样本中，产品环保性能是优等的概率为
，求
，
的值。
件数 | 环保性能 | |||
优等 | 合格 | 不合格 | ||
安全性能 | 优等 | 6 | 20 | 5 |
合格 | 10 | 18 | 6 | |
不合格 |
| 4 |
| |
（3）已知
，
，求在安全性能不合格的产品中，环保性能为优等的件数比不合格的件数少的概率。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知某校6个学生的数学和物理成绩如下表：
学生的编号 | 1 | 2 | 3 | 4 | 5 | 6 |
数学 | 89 | 87 | 79 | 81 | 78 | 90 |
物理 | 79 | 75 | 77 | 73 | 72 | 74 |
（1）若在本次考试中，规定数学在80分以上（包括80分）且物理在75分以上（包括75分）的学生为理科小能手.从这6个学生中抽出2个学生，设
表示理科小能手的人数，求的分布列和数学期望；
（2）通过大量事实证明发现，一个学生的数学成绩和物理成绩具有很强的线性相关关系，在上述表格是正确的前提下，用
表示数学成绩，用
表示物理成绩，求与的回归方程.
参考数据和公式：
，其中
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图,在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,异面直线A1B与B1C1所成的角为60°.
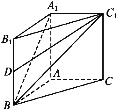
(1)求该三棱柱的体积;
(2)设D是BB1的中点,求DC1与平面A1BC1所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的一个焦点在直线
上，且离心率
.
（1）求该椭圆的方程；
（2）若
与
是该椭圆上不同的两点，且线段
的中点
在直线
上，试证： 
轴上存在定点
，对于所有满足条件的
与
，恒有
；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
为奇函数．
（1）求a的值，并证明
是R上的增函数；
（2）若关于t的不等式f(t2－2t)＋f(2t2－k)＜0的解集非空，求实数k的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】写出下面两个的相关命题的逆命题、否命题、逆否命题，并判断它们的真假：
（1）命题：若
，则
.
逆命题：_______________________________________________________（________）
逆否命题：_____________________________________________________（________）
（2）命题：设
是实数，如果
，那么
有实数根。
否命题：_______________________________________________________（________）
逆否命题：_____________________________________________________（________）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
