
设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并浸入半径为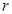 的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?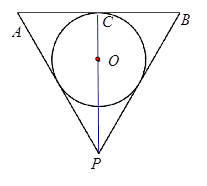
 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:解答题
如图,已知平面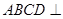 平面
平面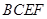 ,且四边形
,且四边形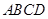 为矩形,四边形
为矩形,四边形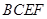 为直角梯形,
为直角梯形,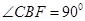 ,
,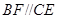 ,
,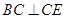 ,
,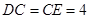 ,
,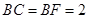 .
.
(1)作出这个几何体的三视图(不要求写作法).
(2)设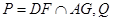 是直线
是直线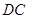 上的动点,判断并证明直线
上的动点,判断并证明直线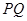 与直线
与直线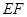 的位置关系.
的位置关系.
(3)求直线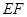 与平面
与平面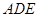 所成角的余弦值.
所成角的余弦值.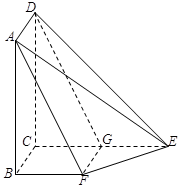
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一个几何体的三视图如图所示.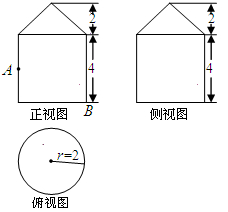
(1)求此几何体的表面积;
(2)在如图的正视图中,如果点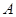 为所在线段中点,点
为所在线段中点,点 为顶点,求在几何体侧面上从点
为顶点,求在几何体侧面上从点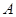 到点
到点 的最短路径的长.
的最短路径的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
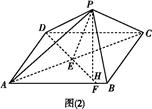
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC 平面ABC,
平面ABC, ,
,

(1)证明:平面ACD 平面ADE;
平面ADE;
(2)记 ,
, 表示三棱锥A-CBE的体积,求函数
表示三棱锥A-CBE的体积,求函数 的解析式及最大值
的解析式及最大值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,矩形ABCD中,AB=a,AD=b,过点D作DE⊥AC于E,交直线AB于F.现将△ACD沿对角线AC折起到△PAC的位置,使二面角P AC
AC B的大小为60°.过P作PH⊥EF于H.
B的大小为60°.过P作PH⊥EF于H.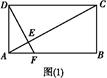
(1)求证:PH⊥平面ABC;
(2)若a+b=2,求四面体P ABC体积的最大值.
ABC体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图1所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4.如图2所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连接AB,设点F是AB的中点.
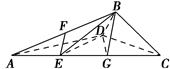
图1 图2
(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥BDEG的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com