
【题目】已知椭圆C: ![]() =1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍.
=1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍. 
(1)求椭圆C的方程;
(2)如图,直线l:y=kx+m与椭圆C相交于P,Q两点,若在椭圆C上存在点R,使OPRQ为平行四边形,求m的取值范围.
【答案】
(1)解:短轴长为2,可得b=1,
即有A(0,1),设F(c,0),B(x0,y0),
△AOF的面积是△BOF的面积的3倍,
即为 ![]() c1=3
c1=3 ![]() c|y0|,
c|y0|,
可得y0=﹣ ![]() ,由直线AF:y=﹣
,由直线AF:y=﹣ ![]() +1经过B,
+1经过B,
可得x0= ![]() c,即B(
c,即B( ![]() c,﹣
c,﹣ ![]() ),代入椭圆方程可得,
),代入椭圆方程可得,
![]() +
+ ![]() =1,即为a2=2c2,即有a2=2b2=2,
=1,即为a2=2c2,即有a2=2b2=2,
则椭圆方程为 ![]() +y2=1
+y2=1
(2)解:设P(x1,y1),Q(x2,y2),
由OPRQ为平行四边形,可得x1+x2=xR,y1+y2=yR,
R在椭圆C上,可得 ![]() +(y1+y2)2=1,
+(y1+y2)2=1,
即为 ![]() +(k(x1+x2)+2m)2=1,
+(k(x1+x2)+2m)2=1,
化为(1+2k2)((x1+x2)2+8km(x1+x2)+8m2=2,①
由 ![]() 可得(1+2k2)x2+4kmx+2m2﹣2=0,
可得(1+2k2)x2+4kmx+2m2﹣2=0,
由△=16k2m2﹣4(1+2k2)(2m2﹣2)>0,即为1+2k2>m2,②
x1+x2=﹣ ![]() ,代入①可得
,代入①可得 ![]() ﹣
﹣ ![]() +8m2=2,
+8m2=2,
化为1+2k2=4m2,代入②可得m≠0,
又4m2=1+2k2≥1,解得m≥ ![]() 或m≤﹣
或m≤﹣ ![]() .
.
则m的取值范围是(﹣∞,﹣ ![]() ]∪[
]∪[ ![]() ,+∞)
,+∞)
【解析】(1)由题意可得b=1,A(0,1),设F(c,0),B(x0 , yspan>0),运用三角形的面积公式可得y0=﹣ ![]() ,再由直线AF的方程经过B,可得B的坐标,代入椭圆方程,解得a,b,进而得到椭圆方程;(2)设P(x1 , y1),Q(x2 , y2),由OPRQ为平行四边形,可得x1+x2=xR , y1+y2=yR , R在椭圆C上,代入椭圆方程,再由直线l与椭圆方程联立,运用韦达定理和判别式大于0,化简整理,解不等式即可得到所求m的范围.
,再由直线AF的方程经过B,可得B的坐标,代入椭圆方程,解得a,b,进而得到椭圆方程;(2)设P(x1 , y1),Q(x2 , y2),由OPRQ为平行四边形,可得x1+x2=xR , y1+y2=yR , R在椭圆C上,代入椭圆方程,再由直线l与椭圆方程联立,运用韦达定理和判别式大于0,化简整理,解不等式即可得到所求m的范围.


科目:高中数学 来源: 题型:
【题目】某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
[20,30) | 30 | 18 |
[30,40) | 36 | 24 |
[40,50) | 12 | 9 |
[50,60] | 4 | 3 |
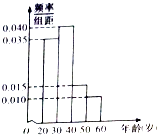
(1)若用分层抽样法从全校教师中抽取一个容量为40的样本,求从年龄段[20,30)抽取的人数;
(2)求全校教师的平均年龄;
(3)随机从年龄段[20,30)和[30,40)内各抽取1人,设这两人中两项培训结业考试成绩都优秀的人数为X,求X的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分位于正方形的中心成中心对称,在正方形内随机取一点,则此点取自黑色部分的概率是( )
内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分位于正方形的中心成中心对称,在正方形内随机取一点,则此点取自黑色部分的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣![]() .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为![]() ,求实数a的值;
,求实数a的值;
(3)若f(x)<x2在(1,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中_________为真命题.
①“A∩B=A”成立的必要条件是“A![]() B”; w ②“若x2+y2=0,则x,y全为0”的否命题;
B”; w ②“若x2+y2=0,则x,y全为0”的否命题;
③“全等三角形是相似三角形”的逆命题; ④“圆内接四边形对角互补”的逆否命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,F1、F2分别是双曲线 ![]() =1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支交于A、B两点,若△F2AB是等边三角形,则双曲线的离心率为 ( )
=1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支交于A、B两点,若△F2AB是等边三角形,则双曲线的离心率为 ( ) 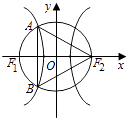
A.![]()
B.2
C.![]() ﹣1
﹣1
D.1+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.
(1)求证:平面PAC⊥平面PBC;
(2)若AC=1,PA=1,求圆心O到平面PBC的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com