
����Ŀ�����г����飬ij��Ʒÿ�ֵļ۸�Ϊx��2��x��14��Ԫʱ������Ʒ���¹�����Ϊy1�֣�y1=ax��16��a��8������������Ϊy2��![]() ��������Ʒ����������С�ڹ�����ʱ�����������ڹ�������������Ʒ��������С�ڹ�����ʱ������������������������Ʒ�������۶�f��x����������������۸�ij˻���
��������Ʒ����������С�ڹ�����ʱ�����������ڹ�������������Ʒ��������С�ڹ�����ʱ������������������������Ʒ�������۶�f��x����������������۸�ij˻���
��1����a=32������Ʒ�ļ۸�Ϊ����Ԫʱ������Ʒ�������۶�f��x�����
��2�����������빩�������ʱ�ļ۸�Ϊ����۸�������Ʒ�ľ���۸���ÿ��10Ԫ����ʵ��a��ȡֵ��Χ��
���𰸡���1��![]() ��2��
��2��![]() .
.
�������������������1����������Ľ���ʽ��ͨ������x�ķ�Χ�Լ������ĵ�����������������ֵ���ɣ�
��2�����ݺ����ĵ����Ե�������a�IJ���ʽ�飬������ɣ�
���������
��1����a=32����y2��y1���é�x2��2x+224��32x��16�� ��é�40��x��6
��Ϊ2��x��14������2��x��6�������Ʒ�������۶�Ϊf��x����
��![]()
�ٵ�2��x��6ʱ��f��x��=��32x��16��x��
����f��x��max=f��6��=1056��Ԫ����
�ڵ�6��x��14ʱ��f��x��=����x2��2x+224��x��
��f'��x��=��3x2��4x+224=����x��8����3x+28����
��f'��x����0����x��8����f�䣨x����0����ã�x��8��
����f��x���ڣ�6��8���������������ڣ�8��14�����Ǽ�������
��x=8ʱ��f��x��max=f��8��=1152��Ԫ������
��Ϊ1152��1056������f��x��max=f��8��=1152Ԫ��
��2����![]() ��
��
��Ϊa��8������g��x�������䣨2��14��������������
������Ʒ�ľ���۸���10Ԫ��
������f��x��������[10��14��������㣬
����![]() ���
���![]() ��
��
����Ϊa��8������8��a��12��


 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д� ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ![]() �У���֪����
�У���֪����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ��
�� ![]() Ϊ������.������ԭ��
Ϊ������.������ԭ��![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���ᣬȡ��ͬ�ij��ȵ�λ����������ϵ��ֱ��
���������Ϊ���ᣬȡ��ͬ�ij��ȵ�λ����������ϵ��ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
����![]() ʱ��������
ʱ��������![]() �ϵĵ㵽ֱ��
�ϵĵ㵽ֱ��![]() �ľ�������ֵ��
�ľ�������ֵ��
����������![]() �ϵ����е㶼��ֱ��
�ϵ����е㶼��ֱ��![]() ���·�����ʵ��
���·�����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=Asin����x+�ȣ��� A��0���أ�0��|��|�� ![]() ������С������Ϊ�У���ͼ������һ����͵�ΪM��
������С������Ϊ�У���ͼ������һ����͵�ΪM�� ![]() ����3����
����3����
��1����f��x���Ľ���ʽ��
��2������f��x����[0����]�ĵ����������䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�߲˻�����ֲ���������������г������֪���Ӷ���һ�����300���ڣ����������ۼ�������ʱ��Ĺ�ϵ��ͼһ��һ�����߱�ʾ������������ֲ�ɱ�������ʱ��Ĺ�ϵ��ͼ���������߶α�ʾ�� 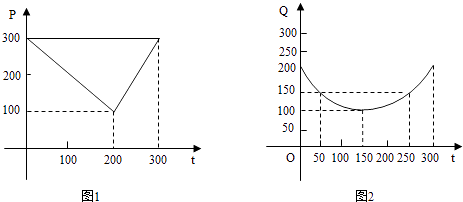
��1��д��ͼһ��ʾ���г��ۼ���ʱ��ĺ�����ϵʽp=f��t����д��ͼ����ʾ����ֲ�ɱ���ʱ��ĺ�����ϵʽQ=g��t����
��2���϶��г��ۼۼ�ȥ��ֲ�ɱ�Ϊ�����棬�ʺ�ʱ���е����������������ע���г��ۼ۸���ֲ�ɱ��ĵ�λ��Ԫ/102�K��ʱ�䵥λ���죩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��y2=2px��p��0���ϵ�һ��M�ĺ�����Ϊ3������ΪF����|MF|=4��ֱ��l��y=2x��4��������C����A��B���㣮
������������C�ķ��̣�
������P��x����һ�㣬�ҡ�PAB���������9�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪p������x2��mx��1��0����������ȵĸ�����q������4x2��4(m��2)x��1��0��ʵ������p��qΪ�棬p��qΪ�٣���m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=2cosxsin��x�� ![]() ��+
��+ ![]() ��
��
��1������f��x���ĶԳ��᷽�̣�
��2��������sin2x+2|f��x+ ![]() ��|��m+1=0��x��[��
��|��m+1=0��x��[�� ![]() ��
�� ![]() ]��������ʵ���⣬��ʵ��m��ȡֵ��Χ��
]��������ʵ���⣬��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ���������ȷ����
�ٺ���y= ![]() �Ķ�������{x|x��0}��
�Ķ�������{x|x��0}��
��lg ![]() =lg��x��2���Ľ⼯Ϊ{3}��
=lg��x��2���Ľ⼯Ϊ{3}��
��31��x��2=0�Ľ⼯Ϊ{x|x=1��log32}��
��lg��x��1����1�Ľ⼯��{x|x��11}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x�� ![]() ��
��
��1���ú��������ԵĶ���֤��������f��x�������䣨0��+�ޣ���Ϊ��������
��2������2tf��4t����mf��2t��=0����t��[1��2]ʱ����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com