
【题目】过直线![]() 上的点
上的点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() ,切点分别为
,切点分别为![]() ,联结
,联结![]() .
.
(1)当点![]() 在直线
在直线![]() 上运动时,证明:直线
上运动时,证明:直线![]() 恒过定点
恒过定点![]() ;
;
(2)当![]() 时,定点
时,定点![]() 平分线段
平分线段![]() .
.
科目:高中数学 来源: 题型:
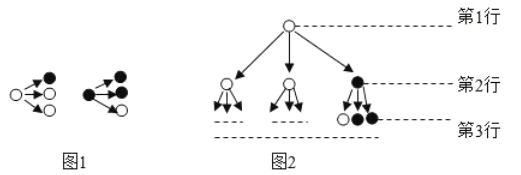
【题目】分形几何学是数学家伯努瓦.曼德尔布罗在20世纪70年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图(1)所示的分形规律可得如图(2)所示的一个树形图.若记图(2)中第![]() 行黑圈的个数为
行黑圈的个数为![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表提供了工厂技术改造后某种型号设备的使用年限![]() 和所支出的维修费
和所支出的维修费![]() (万元)的几组对照数据:
(万元)的几组对照数据:
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
参考公式: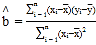 ,
,![]() .
.
(1)若知道![]() 对
对![]() 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知过点![]() 的圆
的圆![]() 和直线
和直线![]() 相切,且圆心在直线
相切,且圆心在直线![]() 上.
上.
(1)求圆![]() 的标准方程;
的标准方程;
(2)点![]() ,圆
,圆![]() 上是否存在点
上是否存在点![]() ,使
,使![]()
![]() 若存在,求出点
若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com