
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
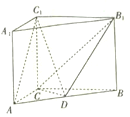
(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知某服装厂每天的固定成本是30000元,每天最大规模的生产量是![]() 件.每生产一件服装,成本增加100元,生产
件.每生产一件服装,成本增加100元,生产![]() 件服装的收入函数是
件服装的收入函数是![]() ,记
,记![]() ,
,![]() 分别为每天生产
分别为每天生产![]() 件服装的利润和平均利润(
件服装的利润和平均利润(![]() ).
).
(1)当![]() 时,每天生产量
时,每天生产量![]() 为多少时,利润
为多少时,利润![]() 有最大值;
有最大值;
(2)每天生产量![]() 为多少时,平均利润
为多少时,平均利润![]() 有最大值,并求
有最大值,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是椭圆![]() 上的动点,
上的动点,![]() 、
、![]() 为椭圆的左、右焦点,O为坐标原点,若M是
为椭圆的左、右焦点,O为坐标原点,若M是![]() 的角平分线上的一点,且F1M⊥MP,则|OM|的取值范围是( )
的角平分线上的一点,且F1M⊥MP,则|OM|的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与相应的生产能耗
吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |

(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知ω>0,0<φ<π,直线![]() 和
和![]() 是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,若将函数f(x)图象上每一点的横坐标变为原来的
是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,若将函数f(x)图象上每一点的横坐标变为原来的![]() 倍,纵坐标变为原来的2倍,则得到的图象的函数解析式是( )
倍,纵坐标变为原来的2倍,则得到的图象的函数解析式是( )
A.![]() B.
B.![]()
C.y=2cos2xD.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2006 年 8 月中旬 , 湖南省资兴市遇到了百年不遇的洪水灾害 . 在资兴市的东江湖岸边的点 O 处(可视湖岸为直线) 停放着一只救人的小船,由于缆绳突然断开,小船被风刮跑,其方向与湖岸成 15°,, 速度为2.5 km/ h ,同时,岸上有一人从同一地点开始追赶小船 .已知他在岸上追的速度为4 km/ h ,在水中游的速度为 2 km/h .问此人能否追上小船? 若小船速度改变 ,则小船能被此人追上的最大速度是多少 ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正多面体共有5种,即正四面体、正六面体、正八面体、正十二面体和正二十面体.任一个正多面体都有内切球和外接球,若一个半径为1的球既是一个正四面体的内切球,又是一个正六面体的外接球,则这两个多面体的顶点之间的最短距离为( )
A.![]() -1B.1C.2
-1B.1C.2![]() -1D.2
-1D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com