
 ,0].
,0]. ,f(B)=-
,f(B)=- ,求:角c的大小.
,求:角c的大小. =2π,ω=
=2π,ω= ,
,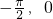 )
) )=0 而-π<φ<0
)=0 而-π<φ<0 .
. )=-cosx
)=-cosx ,cosB=
,cosB= ,又A,B∈(0,π),
,又A,B∈(0,π), ,sinB=
,sinB= ,
,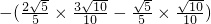 =-
=- ,
, .
. ,0].求出φ,然后求出函数y=f(x)的解析式;
,0].求出φ,然后求出函数y=f(x)的解析式; ,求出cosA,sinA,f(B)=-
,求出cosA,sinA,f(B)=- ,求出cosB,sinB,利用cosC=cos[π-A-B]求出cosC,根据C的范围求角c的大小.
,求出cosB,sinB,利用cosC=cos[π-A-B]求出cosC,根据C的范围求角c的大小.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2n |
 |
| i=1 |
| 2n |
 |
| i=1 |
| 1 | ||
|
查看答案和解析>>
科目:高中数学 来源:2010年全国统一高考数学试卷(文科)(新课标版)(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2012年广东省实验中学考前热身训练数学试卷(理科)(解析版) 题型:解答题
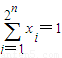 ,证明:
,证明: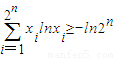
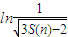 (i,n∈N*).
(i,n∈N*).查看答案和解析>>
科目:高中数学 来源:2010年海南省、宁夏高考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com