
【题目】已知函数f(x)=x2lnx.
(1)求f(x)的单调区间;
(2)证明:![]() .
.
【答案】(1)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增; (2)见解析.
上单调递增; (2)见解析.
【解析】
(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(2)设h(x)=![]() (x>0),根据函数的单调性求出f(x)min>h(x)max,从而证明结论.
(x>0),根据函数的单调性求出f(x)min>h(x)max,从而证明结论.
(1)f′(x)=x(2lnx+1),
令f′(x)=0,解得:x=![]() ,
,
令f′(x)>0,解得:x>![]() ,
,
令f′(x)<0,解得:0<x<![]() ,
,
故f(x)在(0,![]() )递减,在(
)递减,在(![]() ,+∞)递增;
,+∞)递增;
(2)证明:由(1)知当x=![]() 时,f(x)的最小值是﹣
时,f(x)的最小值是﹣![]() ,
,
设h(x)=![]() ﹣
﹣![]() (x>0),则h′(x)=﹣
(x>0),则h′(x)=﹣![]() ,
,
h(x)在(0,2)递增,在(2,+∞)递减,
故h(x)max=h(2)=![]() ﹣
﹣![]() ,
,
∵﹣![]() ﹣(
﹣(![]() ﹣
﹣![]() )=
)=![]() >0,
>0,
∴f(x)min>h(x)max,
故lnx>![]() ﹣
﹣![]() .
.


科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() -
-![]() =1 (a>0,b>0)的左、右焦点分别为F1,F2,点P为双曲线右支上一点,若|PF1|2=8a|PF2|,则双曲线C的离心率的取值范围为( )
=1 (a>0,b>0)的左、右焦点分别为F1,F2,点P为双曲线右支上一点,若|PF1|2=8a|PF2|,则双曲线C的离心率的取值范围为( )
A. (1,3] B. [3,+∞)
C. (0,3) D. (0,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型工厂有6台大型机器,在1个月中,1台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障的概率为![]() .已知1名工人每月只有维修2台机器的能力(若有2台机器同时出现故障,工厂只有1名维修工人,则该工人只能逐台维修,对工厂的正常运行没有任何影响),每台机器不出现故障或出现故障时能及时得到维修,就能使该厂获得10万元的利润,否则将亏损2万元.该工厂每月需支付给每名维修工人1万元的工资.
.已知1名工人每月只有维修2台机器的能力(若有2台机器同时出现故障,工厂只有1名维修工人,则该工人只能逐台维修,对工厂的正常运行没有任何影响),每台机器不出现故障或出现故障时能及时得到维修,就能使该厂获得10万元的利润,否则将亏损2万元.该工厂每月需支付给每名维修工人1万元的工资.
(1)若每台机器在当月不出现故障或出现故障时,有工人进行维修(例如:3台大型机器出现故障,则至少需要2名维修工人),则称工厂能正常运行.若该厂只有1名维修工人,求工厂每月能正常运行的概率;
(2)已知该厂现有2名维修工人.
(ⅰ)记该厂每月获利为![]() 万元,求
万元,求![]() 的分布列与数学期望;
的分布列与数学期望;
(ⅱ)以工厂每月获利的数学期望为决策依据,试问该厂是否应再招聘1名维修工人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是美丽的“勾股树”,它是一个直角三角形分别以它的每一边向外作正方形而得到.图一是第1代“勾股树”,重复图一的作法,得到图二为第2代“勾股树”,以此类推,已知最大的正方形面积为1,则第n代“勾股树”所有正方形的面积的和为( )
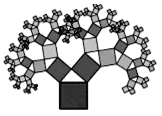
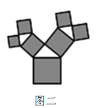
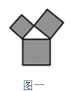
A. nB. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自治区有甲、乙两位航模运动员参加了国家队集训,现分别从他们在集训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲:82 81 79 78 95 88 93 84 乙:92 95 80 75 83 80 90 85
(I)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩中的位数;
(II)现要从中派一人参加国际比赛,从平均成绩和方差的角度考虑,你认为派哪位学生参加合适?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,AB=BC,D、E分别为
中,AB=BC,D、E分别为![]() 的中点.
的中点.

(1)证明:ED为异面直线BB1与AC1的公垂线段;
(2)设AB=1, ![]() ,求二面角A1—AD—C1的大小.
,求二面角A1—AD—C1的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com