
【题目】已知函数f(x)= ![]() (m,n∈R)在x=1处取得极值2.
(m,n∈R)在x=1处取得极值2.
(1)求f(x)的解析式;
(2)k为何值时,方程f(x)﹣k=0只有1个根
(3)设函数g(x)=x2﹣2ax+a,若对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),求a的取值范围.
【答案】
(1)解:因为函数f(1)= ![]() .
.
所以m=2+2n,f(x)= ![]() ,
,
又f(x)在x=1处取得极值,
f  =
= ![]() ,
,
f ![]() ,n=1,则m=4,
,n=1,则m=4,
经检验满足题意,
所以 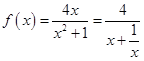 ;
;
(2)解:由f(x)﹣k=0,得k=f(x),
由(1)得f ![]() ,
,
令f′(x)=0,得x=±1.
当x变化时,f′(x),f(x)的变化情况如下表:
x | (﹣∞,﹣1) | ﹣1 | (﹣1,1) | 1 | (1,+∞) |
f'(x) | ﹣ | 0 | + | 0 | ﹣ |
f(x) | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
所以f(x)在x=﹣1处取得极小值﹣2,在x=1处取得极大值2
又 ![]() 如图
如图
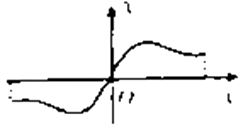
所以k=±2或0时,方程有一个根
(3)解:对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),
只需g(x2)min≤f(x1)min,
即当x∈[﹣1,0]时,x2﹣2ax+a≤﹣2恒成立
只需 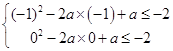 ,
,
解得a≤﹣2
a的取值范围为a≤﹣2
【解析】(1)函数f(1)= ![]() .所以m=2+2n,f(x)=
.所以m=2+2n,f(x)= ![]() ,又f(x)在x=1处取得极值,f
,又f(x)在x=1处取得极值,f ![]() ,n=1,则m=4(2)由f(x)﹣k=0,得k=f(x),由(1)得f
,n=1,则m=4(2)由f(x)﹣k=0,得k=f(x),由(1)得f ![]() ,令f′(x)=0,得x=±1.求出单调区间,根据图象即可求解.(3)对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),只需g(x2)min≤f(x1)min,即当x∈[﹣1,0]时,x2﹣2ax+a≤﹣2恒成立,只需
,令f′(x)=0,得x=±1.求出单调区间,根据图象即可求解.(3)对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),只需g(x2)min≤f(x1)min,即当x∈[﹣1,0]时,x2﹣2ax+a≤﹣2恒成立,只需 ![]() ,解得a.
,解得a.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在每年的春节后,某市政府都会发动公务员参与到植树绿化活动中去.林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):
甲:37,21,31,20,29,19,32,23,25,33;
乙:10,30,47,27,46,14,26,10,44,46.
(1)画出两组数据的茎叶图,并根据茎叶图对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的10株甲种树苗高度平均值为![]() ,将这10株树苗的高度依次输入,按程序框(如图)进行运算,问输出的S大小为多少?并说明S的统计学意义.
,将这10株树苗的高度依次输入,按程序框(如图)进行运算,问输出的S大小为多少?并说明S的统计学意义.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣0.5x+1,则不等式f(2x﹣3)<0.5的解集为( )
A.{x|﹣1<x<1.5}
B.{x|0.5<x<2}
C.{x|x<2}
D.{x|1.5<x<2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.命题“x∈R,使得x2﹣1<0”的否定是:x∈R,均有x2﹣1<0
B.命题“若x=3,则x2﹣2x﹣3=0”的否命题是:若x≠3,则x2﹣2x﹣3≠0
C.“ ![]() ”是“
”是“ ![]() ”的必要而不充分条件
”的必要而不充分条件
D.命题“cosx=cosy,则x=y”的逆否命题是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题
(Ⅰ)某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.设甲、乙两个班所抽取的10名同学成绩方差分别为 ![]() 、
、 ![]() ,比较
,比较 ![]() 、
、 ![]() 的大小(直接写结果,不必写过程);
的大小(直接写结果,不必写过程);
(Ⅱ)设集合 ![]() ,B={x|m+x2≤1,m<1},命题p:x∈A;命题q:x∈B,若p是q的必要条件,求实数m的取值范围.
,B={x|m+x2≤1,m<1},命题p:x∈A;命题q:x∈B,若p是q的必要条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为保障高考的公平性,高考时每个考点都要安装手机屏蔽仪,要求在考点周围1 km内不能收到手机信号.检查员抽查青岛市一考点,在考点正西约![]() km有一条北偏东60°方向的公路,在此处检查员用手机接通电话,以12 km/h的速度沿公路行驶,最长需要多少时间,检查员开始收不到信号,并至少持续多长时间该考点才算合格?
km有一条北偏东60°方向的公路,在此处检查员用手机接通电话,以12 km/h的速度沿公路行驶,最长需要多少时间,检查员开始收不到信号,并至少持续多长时间该考点才算合格?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子商务公司对10 000名网络购物者2017年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
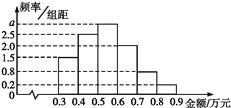
(1)直方图中的a=_____;
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com