练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若，命题；命题直线与圆相交，则 是的

    A．充分不必要条件            B．必要不充分条件

    C．充分必要条件              D．既不充分也不必要条件

    A


    解析:

    A 命题等价于，命题等价于即，显然由命题可得命题，反之不真．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    5、给定下列命题：
    （1）若一直线垂直于一个平面，则此直线垂直于平面内所有直线；
    （2）若一直线平行于一个平面，则此直线平行于平面内无数条直线；
    （3）若一直线与一个平面不垂直，则此直线与平面内所有直线不垂直；
    （4）若一直线与一个平面不平行，则此直线与平面内所有直线不平行，其中错误命题的个数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知抛物线C：y2=2px（p＞0）上任意一点到焦点F的距离比到y轴的距离大1．
    （1）求抛物线C的方程；
    （2）若过焦点F的直线交抛物线于M、N两点，M在第一象限，且|MF|=2|NF|，求直线MN的方程；
    （3）求出一个数学问题的正确结论后，将其作为条件之一，提出与原来问题有关的新问题，我们把它称为原来问题的一个“逆向”问题．
    例如，原来问题是“若正四棱锥底面边长为4，侧棱长为3，求该正四棱锥的体积”．求出体积
    16
    3
    后，它的一个“逆向”问题可以是“若正四棱锥底面边长为4，体积为
    16
    3
    ，求侧棱长”；也可以是“若正四棱锥的体积为
    16
    3
    ，求所有侧面面积之和的最小值”．
    现有正确命题：过点A(-
    p
    2
    ，0)    的直线交抛物线C：y2=2px（p＞0）于P、Q两点，设点P关于x轴的对称点为R，则直线RQ必过焦点F．
    试给出上述命题的“逆向”问题，并解答你所给出的“逆向”问题．

    查看答案和解析>>

    科目：高中数学 来源：学习高手必修二数学苏教版 苏教版 题型：022

    下列命题中，正确命题的序号是________．

    ①直线与平面没有公共点，则直线与平面平行

    ②若直线与平面内的任何一条直线都不相交，则直线与平面平行

    ③若直线与平面内的无数条直线不相交，则直线与平面平行

    ④若两条直线a、b异面，则过b存在唯一一个平面与α平行

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年度新课标高三下学期数学单元测试4-文科 题型：填空题

     下列命题： 

    ①G2=ab是三个数a、G、b成等比数列的充要条件；

    ②若函数y=f（x）对任意实数x都满足f（x+2）=-f（x），则f（x）是周期函数；

    ③对于命题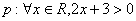,则；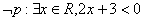

    ④直线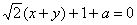与圆C：x2＋y2=a（a>0）相离．

    其中不正确命题的序号为       （把你认为不正确的命题序号都填上）．

     

    查看答案和解析>>

    同步练习册答案