已知:f(x)=ln(1+x)-ln(1-x).
(1)求f(0);
(2)判断此函数的奇偶性;
(3)若f(a)=ln2,求a的值.
【答案】
分析:(1)根据f(x)=ln(1+x)-ln(1-x),可得f(0)=ln(1+0)-ln(1-0),从而得出结果.
(2)求出函数的定义域为(-1,1),再由f(-x)=ln(1-x)-ln(1+x)=-f(x),可知此函数为奇函数.
(3)由f(a)=ln2,可得 ln(1+a)-ln(1-a)=
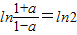
,可得-1<a<1且

,由此求得a的值.
解答:解:(1)因为f(x)=ln(1+x)-ln(1-x),所以f(0)=ln(1+0)-ln(1-0)=0-0=0.
(2)由1+x>0,且1-x>0,知-1<x<1,所以此函数的定义域为:(-1,1).
又f(-x)=ln(1-x)-ln(1+x)=-(ln(1+x)-ln(1-x))=-f(x),由上可知此函数为奇函数.
(3)由f(a)=ln2 知 ln(1+a)-ln(1-a)=

,可得-1<a<1且

,
解得

,
所以a的值为

.
点评:本题主要考查对数的对数和分数指数幂的运算性质的应用,函数的奇偶性的判断,属于基础题.

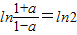 ,可得-1<a<1且
,可得-1<a<1且 ,由此求得a的值.
,由此求得a的值. ,可得-1<a<1且
,可得-1<a<1且 ,
, ,
, .
.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案