
【题目】设有下面四个命题:
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :若
:若![]() ,则
,则![]() .
.
其中的真命题为( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
【答案】C
【解析】分析:根据x<﹣1时,x2+1>2,得出![]() (x2+1)<﹣1,判断
(x2+1)<﹣1,判断![]() 、
、![]() 的正误;
的正误;
根据2sin(α﹣β)=3sin(α+β)=1,求得sinαcosβ的值,判断![]() 、
、![]() 的正误.
的正误.
详解:对于命题![]() :若x<﹣1,则
:若x<﹣1,则![]() >2,
>2,
∴![]() <﹣1,∴
<﹣1,∴![]() 错误;
错误;
对于命题![]() :若2sin(α﹣β)=3sin(α+β)=1,
:若2sin(α﹣β)=3sin(α+β)=1,
则2sinαcosβ﹣2cosαsinβ=1…①,
3sinαcosβ+3cosαsinβ=1 …②,
由①②解得sinαcosβ=![]() ,
,![]() 正确;
正确;
对于命题![]() :若x<﹣1,则x2+1>2,
:若x<﹣1,则x2+1>2,
∴![]() (x2+1)<﹣1,∴
(x2+1)<﹣1,∴![]() 正确;
正确;
对于命题![]() :若2sin(α﹣β)=3sin(α+β)=1,
:若2sin(α﹣β)=3sin(α+β)=1,
则2sinαcosβ﹣2cosαsinβ=1…①,
3sinαcosβ+3cosαsinβ=1 …②,
由①②解得sinαcosβ=![]() ,
,![]() 错误.
错误.
综上,正确的命题是![]() ,
,![]() .
.
故选:C.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,
中,![]() ,不在
,不在![]() 轴上的动点
轴上的动点![]() 满足
满足![]() 于点
于点![]() 为
为![]() 的中点。
的中点。
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设曲线![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,斜率为
,斜率为![]() 的直线交
的直线交![]() 于
于![]() 两点,记直线
两点,记直线![]() 的斜率分别为
的斜率分别为![]() ,试问
,试问![]() 是否为定值?若是,求出该定值;若不是,请说明理由。
是否为定值?若是,求出该定值;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水产试验厂实行某种鱼的人工孵化,10 000个鱼卵能孵化8 513尾鱼苗,根据概率的统计定义解答下列问题:
(1)这种鱼卵的孵化率(孵化概率)是多少?
(2)30 000个鱼卵大约能孵化多少尾鱼苗?
(3)要孵化5 000尾鱼苗,大概需要多少个鱼卵?(精确到百位)
查看答案和解析>>
科目:高中数学 来源: 题型:
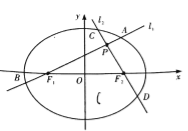
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() , 已知
, 已知![]() 与
与![]() 轴重合时,
轴重合时, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在定点![]() 使得
使得![]() 为定值,若存在,求出
为定值,若存在,求出![]() 点坐标并求出此定值,若不存在,
点坐标并求出此定值,若不存在,
说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》节目组决定把《将进酒》、《山居秋暝》、《望岳》、《送杜少府之任蜀州》和另外确定的两首诗词排在后六场,并要求《将进酒》与《望岳》相邻,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻,且均不排在最后,则后六场开场诗词的排法有_____________种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3200元时,可全部租出。当每辆车的月租金每增加50元时(租金增减为50元的整数倍),未租出的车将会增加一辆。租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)设租金为(3200+50x)元/辆(x∈N),用x表示租赁公司的月收益y(单位:元)。
(3)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com