
【题目】已知数列{an}满足![]() ,且
,且![]() .
.
(1)求证:数列![]() 是等差数列,并求出数列
是等差数列,并求出数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1) an=(2n-1)2n-1;(2) Sn=(2n-3)2n+3.
【解析】
(1)根据等差数列的定义,判断数列![]() 是等差数列,并写出它的通项公式以及{an}的通项公式;
是等差数列,并写出它的通项公式以及{an}的通项公式;
(2)根据数列{an}的前n项和定义,利用错位相减法求出Sn;
(1)证明:因为an=2an-1+2n,所以![]() =
=![]() =
=![]() +1,
+1,
即![]() -
-![]() =1,所以数列
=1,所以数列![]() 是等差数列,且公差d=1,其首项
是等差数列,且公差d=1,其首项![]() =
=![]() ,所以
,所以![]() =
=![]() +(n-1)×1=n-
+(n-1)×1=n-![]() ,解得an=
,解得an=![]() ×2n=(2n-1)2n-1.
×2n=(2n-1)2n-1.
(2)Sn=1×20+3×21+5×22+…+(2n-1)×2n-1,①
2Sn=1×21+3×22+5×23+…+(2n-3)×2n-1+(2n-1)×2n,②
①-②,得-Sn=1×20+2×21+2×22+…+2×2n-1-(2n-1)2n
=1+![]() -(2n-1)2n=(3-2n)2n-3.
-(2n-1)2n=(3-2n)2n-3.
所以Sn=(2n-3)2n+3.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】(请写出式子在写计算结果)有4个不同的小球,4个不同的盒子,现在要把球全部放入盒内:
(1)共有多少种方法?
(2)若每个盒子不空,共有多少种不同的方法?
(3)恰有一个盒子不放球,共有多少种放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l的极坐标方程为θ=α(ρ∈R,ρ≠0),其中α∈[0,π),曲线C1的参数方程为![]() (t为参数),圆C2的普通方程为x2+y2+2
(t为参数),圆C2的普通方程为x2+y2+2![]() x=0.
x=0.
(1)求C1,C2的极坐标方程;
(2)若l与C1交于点A,l与C2交于点B,当|AB|=2时,求△ABC2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了纪念“一带一路”倡议提出五周年,某城市举办了一场知识竞赛,为了了解市民对“一带一路”知识的掌握情况,从回收的有效答卷中按青年组和老年组各随机抽取了40份答卷,发现成绩都在![]() 内,现将成绩按区间
内,现将成绩按区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下的频率分布直方图.
进行分组,绘制成如下的频率分布直方图.
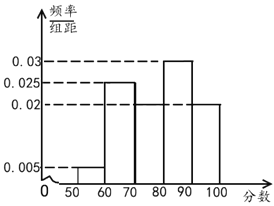
青年组

中老年组
(1)利用直方图估计青年组的中位数和老年组的平均数;
(2)从青年组![]() ,
,![]() 的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自
的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,点
,点![]() 为
为![]() 上异于顶点的任意一点,过
上异于顶点的任意一点,过![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,且有
,且有![]() ,当点
,当点![]() 的横坐标为3时,
的横坐标为3时,![]() 为正三角形.
为正三角形.
(1)求![]() 的方程;
的方程;
(2)若直线![]() ,且
,且![]() 和
和![]() 相切于点
相切于点![]() ,试问直线
,试问直线![]() 是否过定点,若过定点,求出定点坐标;若不过定点,说明理由.
是否过定点,若过定点,求出定点坐标;若不过定点,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com