
【题目】设函数f(x)=ax2-lnx。
(Ⅰ)当a=![]() 时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
【答案】(1)f(x)在0<x≤1上,函数为减函数;在x>1上,函数为增函数;(2)a≤4.
【解析】试题分析:(1)将条件带入求导,得![]() =x-
=x-![]() ,进而根据导数的正负可得函数的单调性;
,进而根据导数的正负可得函数的单调性;
(2)令H(x)= f(x)-(x3+4x-lnx)= -x3+![]() x2-4x=x(-x2+ax-4)所以要使f(x)≤x3+4x-lnx,在定义域内恒成立,只需H(x)≤0,在定义域内恒成立,即x(-x2+ax-4) ≤0在x>0上恒成立,进而转化为-x2+ax-4≤0在x>0上恒成立,进而可得解.
x2-4x=x(-x2+ax-4)所以要使f(x)≤x3+4x-lnx,在定义域内恒成立,只需H(x)≤0,在定义域内恒成立,即x(-x2+ax-4) ≤0在x>0上恒成立,进而转化为-x2+ax-4≤0在x>0上恒成立,进而可得解.
试题解析:
(1)、当a=![]() 时,f(x)=
时,f(x)=![]() x2-lnx,
x2-lnx, ![]() =x-
=x-![]()
令导函数等于0,解得x=1或x=-1(舍),
所以当![]() >0时,x>1,当
>0时,x>1,当![]() <0,0<x<1
<0,0<x<1
所以f(x)在0<x≤1上,函数为减函数;在x>1上,函数为增函数。
(2)令H(x)= f(x)-(x3+4x-lnx)= -x3+![]() x2-4x=x(-x2+ax-4)
x2-4x=x(-x2+ax-4)
所以要使f(x)≤x3+4x-lnx,在定义域内恒成立,只需H(x)≤0,在定义域内恒成立,
即x(-x2+ax-4) ≤0在x>0上恒成立。
由于x>0,所以只要-x2+ax-4≤0在x>0上恒成立
所以应满足△≤0或者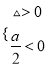 ,所以a≤4.
,所以a≤4.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(3+x)﹣lg(3﹣x)
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并证明;
(3)若f(a)=4,求f(﹣a)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4-4 坐标系与参数方程) 以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为
轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为 (
(![]() 是参数),直线
是参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程和曲线C的普通方程;
的直角坐标方程和曲线C的普通方程;
(2)设点P为曲线C上任意一点,求点P到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床位每天的租金)不超过10元时,床位可以全部租出;当床位高于10元时,每提高1元,将有3张床位空闲. 为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是:①要方便结帐,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高得越多越好.若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入):
(1)把y表示成x的函数;
(2)试确定,该宾馆将床价定为多少元时,既符合上面的两个条件,又能使净收入高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.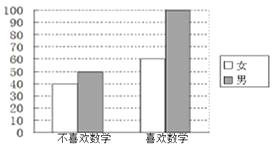
(1)根据二维条形图,完成下表:
男 | 女 | 合计 | |
喜欢数学课程 | |||
不喜欢数学课程 | |||
合计 |
(2)对照如表,利用列联表的独立性检验估计,请问有多大把握认为“性别与喜欢数学有关系”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班学生进行了三次数学测试,第一次有8名学生得满分,第二次有10名学生得满分,第三次有12名学生得满分,已知前两次均为满分的学生有5名,三次测试中至少有一次得满分的学生有15名,若后两次均为满分的学生至少有![]() 名,则
名,则![]() 的值为( )
的值为( )
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC内接于☉O,AB=AC,直线MN切☉O于点C,弦BD∥MN,AC与BD相交于点E. 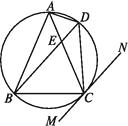
(1)求证:△ABE≌△ACD;
(2)求证:BE=BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com