
【题目】![]() ,
,![]() 为空间中两条互相垂直的直线,等腰直角三角形
为空间中两条互相垂直的直线,等腰直角三角形![]() 的直角边
的直角边![]() 所在直线与
所在直线与![]() ,
,![]() 都垂直,斜边
都垂直,斜边![]() 以直线
以直线![]() 为旋转轴旋转,有下列结论:
为旋转轴旋转,有下列结论:
(1)当直线![]() 与
与![]() 成
成![]() 角时,
角时,![]() 与
与![]() 成
成![]() 角;
角;
(2)当直线![]() 与
与![]() 成
成![]() 角时,
角时,![]() 与
与![]() 成
成![]() 角;
角;
(3)直线![]() 与
与![]() 所成角的最小值为
所成角的最小值为![]() ;
;
(4)直线![]() 与
与![]() 所成角的最小值为
所成角的最小值为![]() ;
;
其中正确的是______(填写所有正确结论的编号).
【答案】(1)(3)
【解析】
由题意知,a、b、AC三条直线两两相互垂直,构建如图所示的边长为1的正方体,|AC|=1,|AB|![]() ,斜边AB以直线AC为旋转轴,则A点保持不变,B点的运动轨迹是以C为圆心,1为半径的圆,以C坐标原点,以CD为x轴,CB为y轴,CA为z轴,建立空间直角坐标系,利用向量法能求出结果.
,斜边AB以直线AC为旋转轴,则A点保持不变,B点的运动轨迹是以C为圆心,1为半径的圆,以C坐标原点,以CD为x轴,CB为y轴,CA为z轴,建立空间直角坐标系,利用向量法能求出结果.
由题意知,a、b、AC三条直线两两相互垂直,画出图形如图,

不妨设图中所示正方体边长为1,
故|AC|=1,|AB|![]() ,
,
斜边AB以直线AC为旋转轴,则A点保持不变,
B点的运动轨迹是以C为圆心,1为半径的圆,
以C坐标原点,以CD为x轴,CB为y轴,CA为z轴,建立空间直角坐标系,
则D(1,0,0),A(0,0,1),直线a的方向单位向量![]() (0,1,0),|
(0,1,0),|![]() |=1,
|=1,
直线b的方向单位向量![]() (1,0,0),|
(1,0,0),|![]() |=1,
|=1,
设B点在运动过程中的坐标中的坐标B′(cosθ,sinθ,0),
其中θ为B′C与CD的夹角,θ∈[0,2π),
∴AB′在运动过程中的向量为![]() (cosθ,sinθ,﹣1),|
(cosθ,sinθ,﹣1),|![]() |
|![]() ,
,
设![]() 与
与![]() 所成夹角为α∈[0,
所成夹角为α∈[0,![]() ],
],
则cosα![]() |sinθ|∈[0,
|sinθ|∈[0,![]() ],
],
∴α∈[![]() ,
,![]() ],∴(3)正确,(4)错误.
],∴(3)正确,(4)错误.
设![]() 与
与![]() 所成夹角为β∈[0,
所成夹角为β∈[0,![]() ],
],
cosβ |cosθ|,
|cosθ|,
当![]() 与
与![]() 夹角为60°时,即α
夹角为60°时,即α![]() ,
,
|sinθ|![]() ,
,
∵cos2θ+sin2θ=1,∴cosβ![]() |cosθ|
|cosθ|![]() ,
,
∵β∈[0,![]() ],∴β
],∴β![]() ,此时
,此时![]() 与
与![]() 的夹角为60°,
的夹角为60°,
∴(1)正确,(2)错误.
故答案为:(1)(3).


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】某学校![]() 、
、![]() 两个班的数学兴趣小组在一次数学对抗赛中的成绩绘制茎叶图如下,通过茎叶图比较两班数学兴趣小组成绩的平均值及方差
两个班的数学兴趣小组在一次数学对抗赛中的成绩绘制茎叶图如下,通过茎叶图比较两班数学兴趣小组成绩的平均值及方差
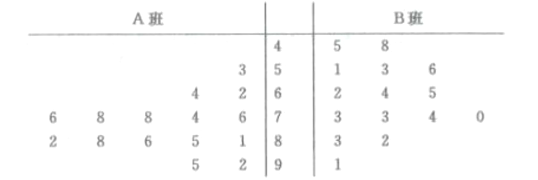
①![]() 班数学兴趣小组的平均成绩高于
班数学兴趣小组的平均成绩高于![]() 班的平均成绩
班的平均成绩
②![]() 班数学兴趣小组的平均成绩高于
班数学兴趣小组的平均成绩高于![]() 班的平均成绩
班的平均成绩
③![]() 班数学兴趣小组成绩的标准差大于
班数学兴趣小组成绩的标准差大于![]() 班成绩的标准差
班成绩的标准差
④![]() 班数学兴趣小组成绩的标准差大于
班数学兴趣小组成绩的标准差大于![]() 班成绩的标准差
班成绩的标准差
其中正确结论的编号为( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() ,且点
,且点![]() 到椭圆C的两焦点的距离之和为
到椭圆C的两焦点的距离之和为![]() .
.

(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ) 若![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个点,线段
上的两个点,线段![]() 的中垂线
的中垂线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 与
与![]() 交于点
交于点![]() ,求证:点
,求证:点![]() 在直线
在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
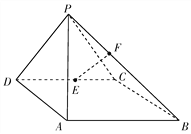
(Ⅰ)求证: ![]() ;
;
(Ⅱ)试确定点![]() 的位置,使得直线
的位置,使得直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等.
所成的角相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:an+1-an=d(n∈N*),前n项和记为Sn,a1=4,S3=21.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足b1=![]() ,bn+1-bn=2an,求数列{bn}的通项公式.
,bn+1-bn=2an,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com