
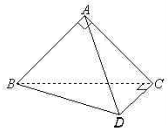
 如图,△ABC与△BCD是一副三角板,它们所在的两个平面互相垂直,且AB=AC,∠BAC=∠BCD=90°,∠CBD=30°.
如图,△ABC与△BCD是一副三角板,它们所在的两个平面互相垂直,且AB=AC,∠BAC=∠BCD=90°,∠CBD=30°.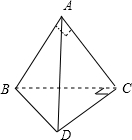 (Ⅰ)证明:如图,
(Ⅰ)证明:如图,| 2 |
2
| ||
| 3 |
| a | ||||
|
| ||
| 4 |
| ||
| 4 |


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
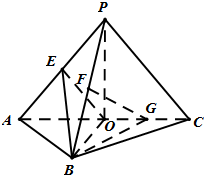 如图,△PAC与△ABC是均以AC为斜边的等腰直角三角形,AC=4,E,F,O分别为PA,PB,AC的中点,G为OC的中点,且PO⊥平面ABC.
如图,△PAC与△ABC是均以AC为斜边的等腰直角三角形,AC=4,E,F,O分别为PA,PB,AC的中点,G为OC的中点,且PO⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:
 [选做题]
[选做题]| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 100 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,△ABC和△A1AC是正三角形,平面A1AC⊥底面ABC,A1B1⊥∥AB,A1B1=AB=2,
如图,△ABC和△A1AC是正三角形,平面A1AC⊥底面ABC,A1B1⊥∥AB,A1B1=AB=2,查看答案和解析>>
科目:高中数学 来源: 题型:
(2)设DEF三等分△ABC所在各边,即BC=3BD,CA=3CE,AB=3AF(如图).

求证:△ABC与△DEF有相同的重心.
查看答案和解析>>
科目:高中数学 来源: 题型:
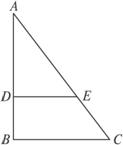
(1)异面直线AD与BC的距离;
(2)二面角A-EC-B的大小(用反三角函数表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com