
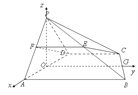
【题目】如图所示,四棱锥![]() 的底面是梯形,且
的底面是梯形,且![]() ,
, ![]() 平面
平面![]() ,
, ![]() 是
是![]() 中点,
中点, ![]() .
.
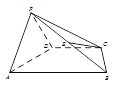
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,
, ![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(I)证明见解析;(II)![]() .
.
【解析】试题分析:(I)取![]() 的中点
的中点![]() ,连结
,连结![]() ,证得
,证得![]() ,从而证得
,从而证得![]() 平面
平面![]() ,根据平行四边形的性质,得
,根据平行四边形的性质,得![]() ,即可证明
,即可证明![]() 平面
平面![]() ;(II)分别以
;(II)分别以![]() 的方向为
的方向为![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() ,求解出平面
,求解出平面![]() 和向量
和向量![]() ,即可利用向量所成的角,得到直线
,即可利用向量所成的角,得到直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
试题解析:(Ⅰ)证明:取![]() 的中点
的中点![]() ,连结
,连结![]() ,如图所示.
,如图所示.
因为![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() .又因为
.又因为![]() ,
,
所以![]() 平面
平面![]() .
.
因为点![]() 是
是![]() 中点,所以
中点,所以![]() ,且
,且![]() .
.
又因为![]() ,且
,且![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,所以
,所以![]() 平面
平面![]() .
.

(Ⅱ)解:设点O,G分别为AD,BC的中点,连结![]() ,则
,则![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() .
.
因为![]() ,由(Ⅰ)知,
,由(Ⅰ)知, ![]() 又因为
又因为![]() ,
,
所以![]() ,所以
,所以![]()
所以![]() 为正三角形,所以
为正三角形,所以![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() .
.
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
故![]() 两两垂直,可以点O为原点,分别以
两两垂直,可以点O为原点,分别以![]() 的方向为
的方向为![]() 轴的正方向,
轴的正方向,
建立空间直角坐标系![]() ,如图所示.
,如图所示.
![]() ,
, ![]() ,
, 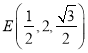 ,
,
所以![]() ,
, ![]() ,
, 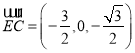 ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则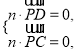 所以
所以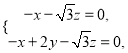 取
取![]() ,则
,则![]() ,
,
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则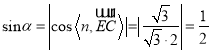 ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
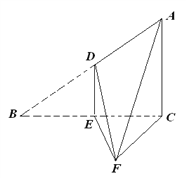
【题目】如图,直角![]() 中,∠
中,∠![]() ,
,![]() ,D、E分别是AB、BC边的中点,沿DE将
,D、E分别是AB、BC边的中点,沿DE将![]() 折起至
折起至![]() ,且∠
,且∠![]() .
.
(Ⅰ)求四棱锥F-ADEC的体积;
(Ⅱ)求证:平面ADF⊥平面ACF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解高三年级学生寒假期间的学习情况,抽取甲、乙两班,调查这两个班的学生在寒假期间每天平均学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生每天平均学习时间在区间[2,4]的有8人.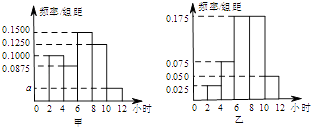
(1)求直方图中a的值及甲班学生每天平均学习时间在区间(10,12]的人数;
(2)从甲、乙两个班每天平均学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中其中真命题个数是( )
①为了了解800名学生的成绩,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40;
②线性回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ;
;
③随机变量ξ服从正态分布N(2,σ2)(σ>0),若在(﹣∞,1)内取值的概率为0.1,则在(2,3)内的概率为0.4;
④若事件![]() 和
和![]() 满足关系
满足关系![]() ,则事件
,则事件![]() 和
和![]() 互斥.
互斥.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,∠PAQ是村里一个小湖的一角,其中∠PAQ=60°.为了给村民营造丰富的休闲环境,村委会决定在直线湖岸AP与AQ上分别建观光长廊AB与AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价预算为12万元(恰好都用完);同时,在线段BC上靠近点B的三等分点D处建一个表演舞台,并建水上通道AD(表演舞台的大小忽略不计),水上通道的造价是600元/米. 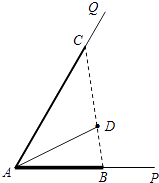
(1)若规划宽长廊AB与窄长廊AC的长度相等,则水上通道AD的总造价需多少万元?
(2)如何设计才能使得水上通道AD的总造价最低?最低总造价是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且垂直于长轴的弦长为
且垂直于长轴的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 分别是椭圆的左、右顶点,若过点
分别是椭圆的左、右顶点,若过点![]() 的直线与椭圆相交于不同两点
的直线与椭圆相交于不同两点![]() .
.
①求证:![]() ;
;
②求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1﹣x)f′(x)的图象如图所示,则下列结论中一定成立的是( ) 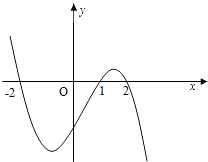
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(﹣2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(﹣2)
D.函数f(x)有极大值f(﹣2)和极小值f(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f'(x)满足2f(x)+xf′(x)>x2(x∈R),则对x∈R都有( )
A.x2f(x)≥0
B.x2f(x)≤0
C.x2[f(x)﹣1]≥0
D.x2[f(x)﹣1]≤0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ax2+x,a∈R.
ax2+x,a∈R.
(1)若f(1)=0,求函数f(x)的最大值;
(2)令g(x)=f(x)﹣(ax﹣1),求函数g(x)的单调区间;
(3)若a=﹣2,正实数x1 , x2满足f(x1)+f(x2)+x1x2=0,证明x1+x2≥ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com