
【题目】甲乙两人参加某种选拔测试,在备选的10道题中,甲答对其中每道题的概率都是![]() ,乙能答对其中的8道题,规定每次考试都从备选的10道题中随机抽出4道题进行测试,只有选中的4个题目均答对才能入选.
,乙能答对其中的8道题,规定每次考试都从备选的10道题中随机抽出4道题进行测试,只有选中的4个题目均答对才能入选.
(1)求甲恰有2个题目答对的概率;
(2)求乙答对的题目数X的分布列;
(3)试比较甲,乙两人平均答对的题目数的大小,并说明理由.
【答案】(1)![]() ;(2)答案见解析;(3)相等,理由见解析;
;(2)答案见解析;(3)相等,理由见解析;
【解析】
(1)根据二项分布概率计算公式,计算出所求概率.
(2)利用超几何分布分布列计算公式,计算出分布列.
(3)由(2)计算出乙平均答对题目数的期望值.利用二项分布期望计算公式,计算出甲平均答对题目数的期望值.由此得到两人平均答对的题目数的大小相等.
(1)∵甲在备选的10道题中,答对其中每道题的概率都是![]() ,
,
∴选中的4个题目甲恰有2个题目答对的概率
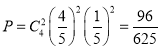 .
.
(2)由题意知乙答对的题目数X的可能取值为2,3,4,
![]() ,
,
![]() ,
,
![]() ,
,
X的分布列为:
X | 2 | 3 | 4 |
P |
|
|
|
(3)∵乙平均答对的题目数![]() ,
,
甲答对题目![]() ,
,
甲平均答对的题目数![]() .
.
![]()
∴甲平均答对的题目数等于乙平均答对的题目数.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】为响应国家“精准扶贫、精准脱贫”的号召,某贫困县在精准推进上下实功,在在精准落实上见实效现从全县扶贫对象中随机抽取![]() 人对扶贫工作的满意度进行调查,以茎叶图中记录了他们对扶贫工作满意度的分数(满分
人对扶贫工作的满意度进行调查,以茎叶图中记录了他们对扶贫工作满意度的分数(满分![]() 分)如图所示,已知图中的平均数与中位数相同.现将满意度分为“基本满意”(分数低于平均分)、“满意”(分数不低于平均分且低于
分)如图所示,已知图中的平均数与中位数相同.现将满意度分为“基本满意”(分数低于平均分)、“满意”(分数不低于平均分且低于![]() 分)和“很满意”(分数不低于
分)和“很满意”(分数不低于![]() 分)三个级别.
分)三个级别.

(1)求茎叶图中数据的平均数和![]() 的值;
的值;
(2)从“满意”和“很满意”的人中随机抽取![]() 人,求至少有
人,求至少有![]() 人是“很满意”的概率.
人是“很满意”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,青蒿素作为一线抗疟药品得到大力推广某农科所为了深入研究海拔因素对青蒿素产量的影响,在山上和山下的试验田中分别种植了![]() 株青蒿进行对比试验.现在从山上和山下的试验田中各随机选取了
株青蒿进行对比试验.现在从山上和山下的试验田中各随机选取了![]() 株青蒿作为样本,每株提取的青蒿素产量(单位:克)如下表所示:
株青蒿作为样本,每株提取的青蒿素产量(单位:克)如下表所示:
编号位置 | ① | ② | ③ | ④ |
山上 |
|
|
|
|
山下 |
|
|
|
|
(1)根据样本数据,试估计山下试验田青蒿素的总产量;
(2)记山上与山下两块试验田单株青蒿素产量的方差分别为![]() ,
,![]() ,根据样本数据,试估计
,根据样本数据,试估计![]() 与
与![]() 的大小关系(只需写出结论);
的大小关系(只需写出结论);
(3)从样本中的山上与山下青蒿中各随机选取![]() 株,记这
株,记这![]() 株的产量总和为
株的产量总和为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面为正方形的四棱锥P-ABCD中,侧棱PD⊥底面ABCD,PD=DC,点E是线段PC的中点.

(1)求异面直线AP与BE所成角的大小;
(2)若点F在线段PB上,使得二面角F-DE-B的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若a,b,c∈R,f(a),f(b),f(c)都是某一三角形的三边长,则称f(x)为“可构造三角形函数”.以下说法正确的是( )
A.f(x)=1(x∈R)不是“可构造三角形函数”
B.“可构造三角形函数”一定是单调函数
C.f(x)=![]() 是“可构造三角形函数”
是“可构造三角形函数”
D.若定义在R上的函数f(x)的值域是![]() (e为自然对数的底数),则f(x)一定是“可构造三角形函数”
(e为自然对数的底数),则f(x)一定是“可构造三角形函数”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com