
【题目】下列说法正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”
”
B.命题“存在![]() ,使得
,使得![]() ”的否定是:“对任意
”的否定是:“对任意![]() ,均有
,均有![]() ”
”
C.命题“角![]() 的终边在第一象限角,则
的终边在第一象限角,则![]() 是锐角”的逆否命题为真命题
是锐角”的逆否命题为真命题
D.已知![]() 是
是![]() 上的可导函数,则“
上的可导函数,则“![]() ”是“
”是“![]() 是函数
是函数![]() 的极值点”的必要不充分条件
的极值点”的必要不充分条件
【答案】D
【解析】
A:根据否命题的定义进行判断即可;
B:根据特称命题的否定性质进行判断即可;
C:根据逆否命题与命题是等价问题,结合第一象限角、锐角的定义进行判断即可;
D:根据必要不充分的定义,结合极值的定义进行判断即可.
A:因为“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ,所以本说法是错误的;
,所以本说法是错误的;
B:因为命题“存在![]() ,使得
,使得![]() ”的否定是:“对任意
”的否定是:“对任意![]() ,均有
,均有
![]() ”,所以本说法是错误的;
”,所以本说法是错误的;
C:因为角![]() 的终边在第一象限角,角
的终边在第一象限角,角![]() 不一定是锐角,例如
不一定是锐角,例如![]() 角的终边在第一象限角,但
角的终边在第一象限角,但![]() 角不是锐角,
角不是锐角,
所以原命题是假命题,又因为原命题的逆否命题与原命题是等价的,因此命题“角![]() 的终边在第一象限角,
的终边在第一象限角,
则![]() 是锐角”的逆否命题为假命题,所以本说法是错误的;
是锐角”的逆否命题为假命题,所以本说法是错误的;
D:由![]() ”不一定能推出“
”不一定能推出“![]() 是函数
是函数![]() 的极值点,例如函数
的极值点,例如函数![]() ,
,
显然![]() ,显然
,显然![]() ,当
,当![]() 时,
时,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() 单调递增,所以
单调递增,所以![]() 不是函数
不是函数![]() 的极值点,
的极值点,
当![]() 是可导函数
是可导函数![]() 的极值点时,一定能推出
的极值点时,一定能推出![]() ,所以已知
,所以已知![]() 是
是![]() 上的可导函数,
上的可导函数,
则“![]() ”是“
”是“![]() 是函数
是函数![]() 的极值点”的必要不充分条件,
的极值点”的必要不充分条件,
因此本说法是正确的.
故选:D


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]()
(1)若![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 的取值范围为______________;
的取值范围为______________;
(2)若对于任意实数![]() ,方程
,方程![]() 有且只有一个实数根,且
有且只有一个实数根,且![]() ,函数
,函数![]() 的图象与函数
的图象与函数![]() 的图象有三个不同的交点,则
的图象有三个不同的交点,则![]() 的取值范围为______________.
的取值范围为______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,∠ABC=60°,AA1![]() AB,M,N分别为AB,AA1的中点.
AB,M,N分别为AB,AA1的中点.
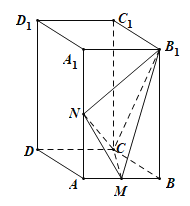
(1)求证:平面B1NC⊥平面CMN;
(2)若AB=2,求点N到平面B1MC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某购物商场分别推出支付宝和微信“扫码支付”购物活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用“扫码支付”.现统计了活动刚推出一周内每天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次,统计数据如下表所示:
表示每天使用扫码支付的人次,统计数据如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据散点图判断,在推广期内,扫码支付的人![]() 次关于活动推出天数
次关于活动推出天数![]() 的回归方程适合用
的回归方程适合用![]() 来表示,求出该回归方程,并预测活动推出第
来表示,求出该回归方程,并预测活动推出第![]() 天使用扫码支付的人次;
天使用扫码支付的人次;
(2)推广期结束后,商场对顾客的支付方式进行统计,结果如下表:
支付方式 | 现金 | 会员卡 | 扫码 |
比例 |
|
|
|
商场规定:使用现金支付的顾客无优惠,使用会员卡支付的顾客享受![]() 折优惠,扫码支付的顾客随机优惠,根据统计结果得知,使用扫码支付的顾客,享受
折优惠,扫码支付的顾客随机优惠,根据统计结果得知,使用扫码支付的顾客,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() .现有一名顾客购买了
.现有一名顾客购买了![]() 元的商品,根据所给数据用事件发生的频率来估计相应事件发生的概率,估计该顾客支付的平均费用是多少?
元的商品,根据所给数据用事件发生的频率来估计相应事件发生的概率,估计该顾客支付的平均费用是多少?
参考数据:设![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: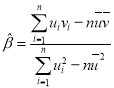 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() -2为自然对数的底数,
-2为自然对数的底数,![]() ).
).
(1)若曲线![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() 至多有一个公共点时,求
至多有一个公共点时,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,若函数
时,若函数![]() 有两个零点,求
有两个零点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,且
轴上,且![]() ,
,![]() ,当点
,当点![]() 在
在![]() 轴上运动时,动点
轴上运动时,动点![]() 的轨迹为曲线
的轨迹为曲线![]() .过
.过![]() 轴上一点
轴上一点![]() 的直线交曲线
的直线交曲线![]() 于
于![]() ,
,![]() 两点.
两点.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)证明:存在唯一的一点![]() ,使得
,使得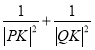 为常数,并确定
为常数,并确定![]() 点的坐标.
点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com