
【题目】设全集![]() .
.
(1)解关于![]() 的不等式
的不等式![]() ;
;
(2)记![]() 为(1)中不等式的解集,
为(1)中不等式的解集,![]() 为不等式组
为不等式组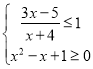 的整数解集,若
的整数解集,若![]() 恰有三个元素,求
恰有三个元素,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某学校科技节需要同学设计一幅矩形纸板宣传画,要求画面的面积为![]() (如图中的阴影部分),画面的上、下各留
(如图中的阴影部分),画面的上、下各留![]() 空白,左、右各留
空白,左、右各留![]() 空白.
空白.
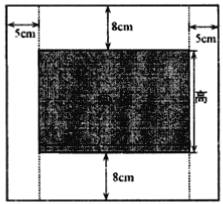
(1)如何设计画面的高与宽的尺寸,才能使整个宣传画所用纸张面积最小?
(2)如果按照第一问这样制作整个宣传画,在科技节结束以后,这整个宣传画纸板可再次作为某实验道具,并要求从整个宣传画板的四个角各截取一个相同的小正方形,做成一个长方体形的无盖容器.问截下的小正方形的边长(也就是该容器的高)是多少时,该容器的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M=![]() ,对它的非空子集A,可将A中每个元素K都乘以
,对它的非空子集A,可将A中每个元素K都乘以![]() 再求和(如A=
再求和(如A=![]() ,可求得和为
,可求得和为![]() ),则对M的所有非空子集,这些和的总和是__________________.
),则对M的所有非空子集,这些和的总和是__________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (t为参数),直线
(t为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).设
为参数).设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时,![]() 的轨迹为曲线
的轨迹为曲线![]()
(1)写出![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,设
轴正半轴为极轴建立极坐标系,设![]() ,
,![]() 为
为![]() 与
与![]() 的交点,求
的交点,求![]() 的极径.
的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2019年春季以来,在非洲猪瘟、环保禁养、上行周期等因素形成的共振条件下,猪肉价格连续暴涨.某养猪企业为了抓住契机,决定扩大再生产,根据以往的养猪经验预估:在近期的一个养猪周期内,每养![]() 百头猪
百头猪![]() ,所需固定成本为20万元,其它为变动成本:每养1百头猪,需要成本14万元,根据市场预测,销售收入
,所需固定成本为20万元,其它为变动成本:每养1百头猪,需要成本14万元,根据市场预测,销售收入![]() (万元)与
(万元)与![]() (百头)满足如下的函数关系:
(百头)满足如下的函数关系:![]() (注:一个养猪周期内的总利润
(注:一个养猪周期内的总利润![]() (万元)=销售收入-固定成本-变动成本).
(万元)=销售收入-固定成本-变动成本).
(1)试把总利润![]() (万元)表示成变量
(万元)表示成变量![]() (百头)的函数;
(百头)的函数;
(2)当![]() (百头)为何值时,该企业所获得的利润最大,并求出最大利润.
(百头)为何值时,该企业所获得的利润最大,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点,与抛物线的准线相交于点
两点,与抛物线的准线相交于点![]() ,
, ![]() ,则
,则![]() 与
与![]() 的面积之比
的面积之比![]() __________.
__________.
【答案】![]()
【解析】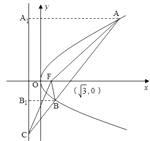
由题意可得抛物线的焦点![]() 的坐标为
的坐标为![]() ,准线方程为
,准线方程为![]() 。
。
如图,设![]() ,过A,B分别向抛物线的准线作垂线,垂足分别为E,N,则
,过A,B分别向抛物线的准线作垂线,垂足分别为E,N,则
![]() ,解得
,解得![]() 。
。
把![]() 代入抛物线
代入抛物线![]() ,解得
,解得![]() 。
。
∴直线AB经过点![]() 与点
与点![]() ,
,
故直线AB的方程为![]() ,代入抛物线方程解得
,代入抛物线方程解得![]() 。
。
∴![]() 。
。
在![]() 中,
中, ![]() ,
,
∴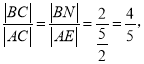
∴![]() 。答案:
。答案: ![]()
点睛:
在解决与抛物线有关的问题时,要注意抛物线的定义在解题中的应用。抛物线定义有两种用途:一是当已知曲线是抛物线时,抛物线上的点M满足定义,它到准线的距离为d,则|MF|=d,可解决有关距离、最值、弦长等问题;二是利用动点满足的几何条件符合抛物线的定义,从而得到动点的轨迹是抛物线.
【题型】填空题
【结束】
17
【题目】已知![]() 三个内角
三个内角![]() 所对的边分别是
所对的边分别是![]() ,若
,若![]() .
.
(1)求角![]() ;
;
(2)若![]() 的外接圆半径为2,求
的外接圆半径为2,求![]() 周长的最大值.
周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() 为棱
为棱![]() 的中点.
的中点.![]() ,
,![]() ,
,![]() .
.
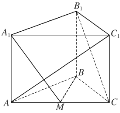
(1)求证:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?如果存在,求此时
?如果存在,求此时![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com