练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知椭圆C:,点M(2,1).
    （1）求椭圆C的焦点坐标和离心率；
    （2）求通过M点且被这点平分的弦所在的直线方程.
    （1）焦点坐标是 离心率
    （2）
    (1)由椭圆方程可得a,b,c的值，进而可求出其焦点坐标及e.
    (2)显然直线的斜率存在，设此直线方程为，且它与椭圆的交点分别为A(x1，y1)、B(x2，y2),代入椭圆方程后作差分解因式，利用代点相减的方法可得斜经k的值。从而直线方程确定
    （1）由 得 …………2分
    所以 焦点坐标是………3分  离心率……………4分
    （2）显然直线不与x轴垂直，可设此直线方程为，且它与椭圆的交点分别为A(x1，y1)、B(x2，y2)，则…………………6分
    所以：…………8分
    又    ，所以：，直线方程为：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    如图，一种电影放映灯的反射镜面是旋转椭圆面的一部分．

    过对称轴的截口是椭圆的一部分，灯丝位于椭圆的一个焦点上，片门位于另一个焦点上，由椭圆一个焦点发出的光线，经过旋转椭圆面反射后集中到另一个焦点．已知，，试建立适当的坐标系，求截口所在椭圆的方程．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    为了加快经济的发展，某市选择A、B两区作为龙头带动周边地区的发展，决定在A、B两区的周边修建城际快速通道，假设A、B两区相距个单位距离，城际快速通道所在的曲线为E，使快速通道E上的点到两区的距离之和为4个单位距离.

    （Ⅰ）以线段AB的中点O为原点建立如图所示的直角坐标系，求城际快速通道所在曲线E的方程；
    （Ⅱ）若有一条斜率为的笔直公路l与曲线E交于P，Q两点，同时在曲线E上建一个加油站M（横坐标为负值）满足,求面积的最大值．                               

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

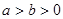    如图，在平面直角坐标系xOy中， 点A为椭圆E：（）的左顶点， B，C在椭圆E上，若四边形OABC为平行四边形，且∠OAB＝30°，则椭圆E的离心率等于       .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知椭圆的一个焦点为F（2，0），离心率.
    (1)求椭圆的方程;
    (2)设直线与椭圆交于不同的A,B两点,与y轴交于E点,且,求实数m的值.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    椭圆上的点到直线的最大距离为（    ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    动点A到定点和的距离的和为4，则动点A的轨迹为 (     )
    A．椭圆B．线段C．无图形D．两条射线；

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    设是椭圆的两个焦点，是椭圆上的动点（不能重合于长轴的两端点），是的内心，直线交轴于点，则       

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    椭圆的焦点为和，过点的直线交椭圆于两点，，则椭圆的离心率为（    ）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案