
【题目】设椭圆![]() 的一个焦点为
的一个焦点为![]() ,四条直线
,四条直线![]() ,
,![]() 所围成的区域面积为
所围成的区域面积为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设过![]() 的直线
的直线![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,设弦
,设弦![]() 的中点为
的中点为![]() ,且
,且![]() (
(![]() 为原点),求直线
为原点),求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果前一个人10分钟内不能完成任务则撤出,再派下一个人.现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别为![]() ,
,![]() ,
,![]() ,假设
,假设![]() ,
,![]() ,
,![]() 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(1)如果按甲最先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)假定![]() ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的数学期望达到最小.
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的数学期望达到最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
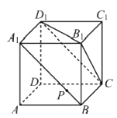
【题目】如图,在正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上移动,有下列判断:①平面
上移动,有下列判断:①平面![]() 平面
平面![]() ;②平面
;②平面![]() 平面
平面![]() ;③三棱锥
;③三棱锥![]() 的体积不变;④
的体积不变;④![]() 平面
平面![]() .其中,正确的是______.(把所有正确的判断的序号都填上)
.其中,正确的是______.(把所有正确的判断的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.“![]() 为真”是“
为真”是“![]() 为真”的充分不必要条件;
为真”的充分不必要条件;
B.若数据![]() 的平均数为1,则
的平均数为1,则![]() 的平均数为2;
的平均数为2;
C.在区间![]() 上随机取一个数
上随机取一个数![]() ,则事件“
,则事件“![]() ”发生的概率为
”发生的概率为![]()
D.设从总体中抽取的样本为![]() 若记样本横、纵坐标的平均数分别为
若记样本横、纵坐标的平均数分别为![]() ,则回归直线
,则回归直线![]() 必过点
必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若满足
,若满足![]() ,则称数列
,则称数列![]() 为“0-1数列”.定义变换
为“0-1数列”.定义变换![]() ,
,![]() 将“0-1数列”
将“0-1数列”![]() 中原有的每个1都变成0,1,原有的每个0都变成1,0.例如
中原有的每个1都变成0,1,原有的每个0都变成1,0.例如![]() :1,0,1,则
:1,0,1,则![]() 设
设![]() 是“0-1数列”,令
是“0-1数列”,令![]()
![]() 3,….
3,….
(Ⅰ) 若数列![]() :
:![]() 求数列
求数列![]() ;
;
(Ⅱ) 若数列![]() 共有10项,则数列
共有10项,则数列![]() 中连续两项相等的数对至少有多少对?请说明理由;
中连续两项相等的数对至少有多少对?请说明理由;
(Ⅲ)若![]() 为0,1,记数列
为0,1,记数列![]() 中连续两项都是0的数对个数为
中连续两项都是0的数对个数为![]() ,
,![]() .求
.求![]() 关于
关于![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市房管局为了了解该市市民![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间买二手房情况,首先随机抽样其中
月期间买二手房情况,首先随机抽样其中![]() 名购房者,并对其购房面积
名购房者,并对其购房面积![]() (单位:平方米,
(单位:平方米,![]() )进行了一次调查统计,制成了如图
)进行了一次调查统计,制成了如图![]() 所示的频率分布直方图,接着调查了该市
所示的频率分布直方图,接着调查了该市![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间当月在售二手房均价
月期间当月在售二手房均价![]() (单位:万元/平方米),制成了如图
(单位:万元/平方米),制成了如图![]() 所示的散点图(图中月份代码
所示的散点图(图中月份代码![]() 分别对应
分别对应![]() 年
年![]() 月至
月至![]() 年
年![]() 月).
月).
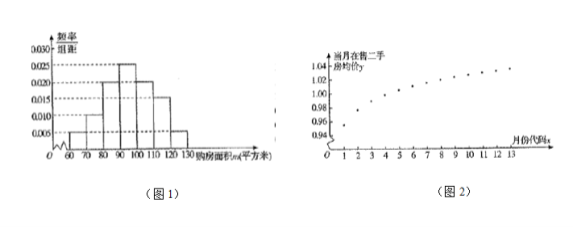
(1)试估计该市市民的购房面积的中位数![]() ;
;
(2)现采用分层抽样的方法从购房面积位于![]() 的
的![]() 位市民中随机抽取
位市民中随机抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人,求这
人,求这![]() 人的购房面积恰好有一人在
人的购房面积恰好有一人在![]() 的概率;
的概率;
(3)根据散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程,分别为
两个模型进行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值如下表所示:
,并得到一些统计量的值如下表所示:
|
| |
| 0.000591 | 0.000164 |
| 0.006050 | |
请利用相关指数![]() 判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出
判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出![]() 年
年![]() 月份的二手房购房均价(精确到
月份的二手房购房均价(精确到![]() )
)
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(参考公式)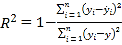
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,展现中国文化阴阳转化、对立统一的哲学理念.定义:图象能将圆的周长和面积同时等分成两部分的函数称为圆的一个“太极函数”,则下列命题正确的是___________.

(1)函数![]() 可以同时是无数个圆的“太极函数”;
可以同时是无数个圆的“太极函数”;
(2)函数![]() 可以是某个圆的“太极函数”;
可以是某个圆的“太极函数”;
(3)若函数![]() 是某个圆的“太极函数”,则函数
是某个圆的“太极函数”,则函数![]() 的图象一定是中心对称图形;
的图象一定是中心对称图形;
(4)对于任意一个圆,其“太极函数”有无数个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com