
分析 (1)通过讨论x的范围,求出各个区间上的x的范围,取并集即可;(2)根据绝对值的性质得到关于a的不等式,解出即可.
解答 解:(1)$f(x)=\left\{{\begin{array}{l}{2x-2,x≥3}\\{4,-1<x<3}\\{-2x+2,x≤-1}\end{array}}\right.$,
当x≥3时,2x-2≥6解得x≥4,
当-1<x<3时,4≥6无解,
当x≤-1时,-2x+2≥6解得x≤-2.
∴f(x)≥6的解集为{x|x≤-2或x≥4}.
(2)由已知|x-3|+|x+1|≥|x+1|-|x+a|-a恒成立,
∴|x-3|+|x+a|≥-a恒成立,
又|x-3|+|x+a|≥|x-3-x-a|=|-3-a|=|a+3|,
∴|a+3|≥-a,
解得$a≥-\frac{3}{2}$,
∴$a∈[{-\frac{3}{2},+∞})$时,不等式f(x)≥g(x)恒成立.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
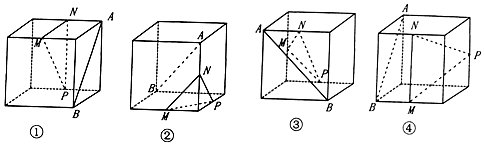
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | 1+$\sqrt{3}$ | D. | 2+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
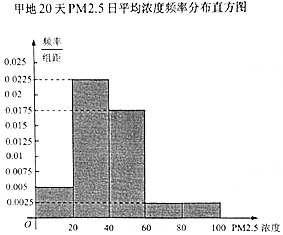
| PM2.5日平均浓度(微克/立方米) | [0,20] | (20,40] | (40,60] | (60,80] | (80,100] |
| 频数(天) | 2 | 3 | 4 | 6 | 5 |
| 满意度等级 | 非常满意 | 满意 | 不满意 |
| PM2.5日平均浓度(微克/立方米) | 不超过20 | 大于20不超过60 | 超过60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 120 | B. | 105 | C. | 153 | D. | 91 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com