
【题目】如图,已知三棱柱ABC﹣A1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点.
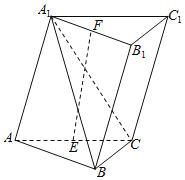
(1)证明:EF⊥BC;
(2)求直线EF与平面A1BC所成角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)方法一:连接![]() ,证明BC⊥平面A1EF,从而EF⊥BC;
,证明BC⊥平面A1EF,从而EF⊥BC;
方法二:由条件证明A1E⊥平面ABC,以E为原点,建立如图空间直角坐标系
计算![]() ,从而EF⊥BC.
,从而EF⊥BC.
(2)方法一:取BC中点G,连结EG、GF,证明平面A1BC⊥平面EGFA,从而确定∠EOG是直线EF与平面A1BC所成角(或其补角),运用余弦定理求得cos∠EOG,最终得出答案.
方法二:建立空间直角坐标系,先求出平面A1BC的法向量![]() ,利用向量
,利用向量![]() 与
与![]() 的夹角为所求角的正弦,即可求出.
的夹角为所求角的正弦,即可求出.
方法一:
证明:(1)连结A1E,∵A1A=A1C,E是AC的中点,
∴A1E⊥AC,
又平面A1ACC1⊥平面ABC,A1E平面A1ACC1,
平面A1ACC1∩平面ABC=AC,
∴A1E⊥平面ABC,∴A1E⊥BC,
∵A1F∥AB,∠ABC=90°,∴BC⊥A1F,
∴BC⊥平面A1EF,∴EF⊥BC.
解:(2)取BC中点G,连结EG、GF,则EGFA1是平行四边形,
由于A1E⊥平面ABC,故A1E⊥EG,
∴平行四边形EGFA1是矩形,
由(1)得BC⊥平面EGFA1,
则平面A1BC⊥平面EGFA1,
∴EF在平面A1BC上的射影在直线A1G上,
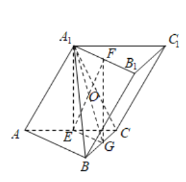
连结A1G,交EF于O,则∠EOG是直线EF与平面A1BC所成角(或其补角),
不妨设AC=4,则在Rt△A1EG中,A1E=2![]() ,EG=
,EG=![]() ,
,
∵O是A1G的中点,故![]() ,
,
∴cos∠EOG![]() ,
,
∴直线EF与平面A1BC所成角的余弦值为![]() .
.
方法二:
证明:(1)连结A1E,∵A1A=
∴A1E⊥AC,
又平面A1ACC1⊥平面ABC,A1E平面A1ACC1,
平面A1ACC1∩平面ABC=AC,
∴A1E⊥平面ABC,
如图,以E为原点,在平面ABC中,过E作AC的垂线为x轴,
EC,EA1所在直线分别为y,z轴,建立空间直角坐标系,
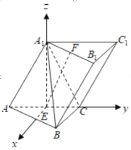
设AC=4,则A1(0,0,2![]() ),B(
),B(![]() ),B1(
),B1(![]() ),F(
),F(![]() ),C(0,2,0),
),C(0,2,0),
![]() (
(![]() ),
),![]() (
(![]() )
)
由![]() 0,得EF⊥BC.
0,得EF⊥BC.
解:(2))设直线EF与平面A1BC所成角为θ,
由(1)得![]() (
(![]() ),
),![]() (0,2,﹣2
(0,2,﹣2![]() ),
),
设平面A1BC的法向量![]() (x,y,z),
(x,y,z),
则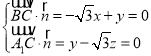 ,取x=1,得
,取x=1,得![]() (1,
(1,![]() ),
),
∴sinθ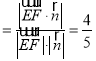 ,
,
∴直线EF与平面A1BC所成角的余弦值为![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】随着银行业的不断发展,市场竞争越来越激烈,顾客对银行服务质量的要求越来越高,银行为了提高柜员,员工的服务意识,加强评价管理,工作中让顾客对服务作出评价,评价分为满意、基本满意、不满意三种,某银行为了比较顾客对男女柜员员工满意度评价的差异,在下属的四个分行中随机抽出40人(男女各半)进行分析比较对40人一月中的顾客评价“不满意“的次数进行了统计,按男、女分为两组,再将每组柜员员工的月“不满意”次数分为5组:[0,5),[5,10),[10,15),[15,20),[20,25],得到如下频数分布表.
分组 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25] |
女柜员 | 2 | 3 | 8 | 5 | 2 |
男柜员 | 1 | 3 | 9 | 4 | 3 |
(1)在答题卡所给的坐标系中分别画出男、女柜员员工的频率分布直方图;并求出男、女柜员的月平均“不满意”次数的估计值,试根据估计值比较男、女柜员的满意度谁高?
(2)在抽取的40名柜员员工中,从“不满意”次数不少于20的柜员员工中随机抽取3人,求抽取的3人中,男柜员不少于女柜员的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() 是坐标原点,若
是坐标原点,若![]() ,且
,且![]() 方向是沿
方向是沿![]() 的方向绕着
的方向绕着![]() 点按逆时针方向旋转
点按逆时针方向旋转![]() 角得到的,则称
角得到的,则称![]() 经过一次
经过一次![]() 变换得到
变换得到![]() ,现有向量
,现有向量![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,
,![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,…,如此下去,
,…,如此下去,![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,设
,设![]() ,
,![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A.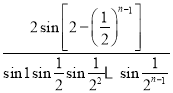 B.
B.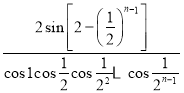
C.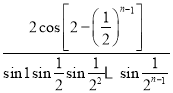 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】故宫博物院五一期间同时举办“戏曲文化展”、“明代御窖瓷器展”、“历代青绿山水画展”、 “赵孟頫书画展”四个展览.某同学决定在五一当天的上、下午各参观其中的一个,且至少参观一个画展,则不同的参观方案共有
A. 6种 B. 8种 C. 10种 D. 12种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 在
在![]() 的单调区间;
的单调区间;
(Ⅱ)方程![]() 有3个不同的实根,求实数
有3个不同的实根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,若对于任意的
时,若对于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求满足条件的正整数
,求满足条件的正整数![]() 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为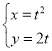 (t为参数),直线
(t为参数),直线![]() 过点
过点![]() 且倾斜角为
且倾斜角为![]() ,以坐标原点O为极点,x轴正半轴为极轴,取相同的单位长度建立极坐标系.
,以坐标原点O为极点,x轴正半轴为极轴,取相同的单位长度建立极坐标系.
(1)写出曲线C的极坐标方程和直线![]() 的参数方程;
的参数方程;
(2)若直线l与曲线C交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左右顶点,
的左右顶点,![]() 点为椭圆
点为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,且
,且![]() .
.
(1)若椭圆![]() 经过圆
经过圆![]() 的圆心,求椭圆
的圆心,求椭圆![]() 的方程;
的方程;
(2)在(1)的条件下,若过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的
相交于不同的![]() 两点,设
两点,设![]() 为椭圆
为椭圆![]() 上一点,且满足
上一点,且满足![]() (
(![]() 为坐标原点),当
为坐标原点),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为![]() 的正方体
的正方体![]() 中,O是AC的中点,E是线段D1O上一点,且D1E=λEO.
中,O是AC的中点,E是线段D1O上一点,且D1E=λEO.
(1)若λ=1,求异面直线DE与CD1所成角的余弦值;
(2)若平面CDE⊥平面CD1O,求λ的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com