
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)令$g(x)=f(x)-[{({\frac{a}{2}-1}){x^2}+ax-1}]=lnx-\frac{1}{2}a{x^2}+({1-a})x+1$,求出函数的导数,得到函数的单调区间,求出函数的最大值,从而证出结论即可;
(3)得到(x1+x2)2+(x1+x2)=x1x2-ln(x1x2),这样令t=x1x2,t>0,容易求得函数t-lnt的最小值为1,从而得到(x1+x2)2+(x1+x2)≥1,解这个关于x1+x2的一元二次不等式即可得出要证的结论.
解答 解:(1)$f'(x)=\frac{1}{x}-2x+1=\frac{{-2{x^2}+x+1}}{x}({x>0})$,
由f'(x)<0,得2x2-x-1>0.又x>0,所以x>1,
所以f(x)的单调递减区间为(1,+∞),函数f(x)的单增区间为(0,1).
(2)令$g(x)=f(x)-[{({\frac{a}{2}-1}){x^2}+ax-1}]=lnx-\frac{1}{2}a{x^2}+({1-a})x+1$,
所以$g'(x)=\frac{1}{x}-ax+({1-a})=\frac{{-a{x^2}+({1-a})x+1}}{x}$,
因为a≥2,所以$g'(x)=-\frac{{a({x-\frac{1}{a}})({x+1})}}{x}$,
令g'(x)=0,得$x=\frac{1}{a}$,所以当$x=({0,\frac{1}{a}}),g'(x)>0$,当$x∈({\frac{1}{a},+∞})$时,g'(x)<0,
因此函数g(x)在$x∈({0,\frac{1}{a}})$是增函数,在$x∈({\frac{1}{a},+∞})$是减函数,
故函数g(x)的最大值为$g({\frac{1}{a}})=ln({\frac{1}{a}})-\frac{1}{2}a×{({\frac{1}{a}})^2}+({1-a})×({\frac{1}{a}})+1=\frac{1}{2a}-lna$,
令$h(a)=({\frac{1}{2a}})-lna$,因为$h(2)=\frac{1}{4}-ln2<0$,又因为h(a)在a∈(0,+∞)是减函数,
所以当a≥2时,h(a)<0,即对于任意正数x总有g(x)<0,
所以关于x的不等式恒成立.
(3)由f(x1)+f(x2)+2(${{x}_{1}}^{2}$+${{x}_{2}}^{2}$)+x1x2=0,
即lnx1+${{x}_{1}}^{2}$+lnx2+${{x}_{2}}^{2}$+x1x2=0,
从而${{(x}_{1}{+x}_{2})}^{2}$+(x1+x2)=x1x2-ln(x1x2),
令t=x1x2,则由h(t)=t-lnt得,h′(t)=$\frac{t-1}{t}$,
可知,h(t)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,
∴h(t)≥h(1)=1,
∴(x1+x2)2+(x1+x2)≥1,又x1+x2>0,
因此x1+x2≥$\frac{\sqrt{5}-1}{2}$成立.
点评 本题考查了函数的单调性问题,考查导数的应用以及换元思想,考查不等式的证明,是一道中档题.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $[2-\frac{{2\sqrt{3}}}{3},2+\frac{{2\sqrt{3}}}{3}]$ | B. | $[1,2+\frac{{2\sqrt{3}}}{3}]$ | C. | $[2-\frac{{2\sqrt{3}}}{3},3]$ | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
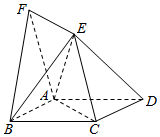 如图,正方形ABCD和菱形ACEF所在平面互相垂直,∠ACE=60°.四棱锥E-ABCD的体积是36$\sqrt{6}$.
如图,正方形ABCD和菱形ACEF所在平面互相垂直,∠ACE=60°.四棱锥E-ABCD的体积是36$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是偶函数但不是奇函数 | B. | 是奇函数但不是偶函数 | ||
| C. | 是非奇非偶函数 | D. | 可能是奇函数也可能是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
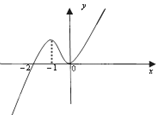 已知在R上可导的函数f(x)的图象如图所示,则不等式f(x)•f′(x)<0的解集为( )
已知在R上可导的函数f(x)的图象如图所示,则不等式f(x)•f′(x)<0的解集为( )| A. | (-2,0) | B. | (-∞,-2)∪(-1,0) | C. | (-∞,-2)∪(0,+∞) | D. | (-2,-1)∪(0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com