
科目:高中数学 来源: 题型:解答题
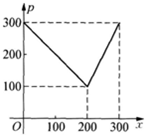 根据历年市场行情得知,从2月1日起的300天内,某种蔬菜的市场售价p与上市时间x的关系图是一条折线(如图),写出这种蔬菜的市场售价与时间的函数解析式p=p(x).
根据历年市场行情得知,从2月1日起的300天内,某种蔬菜的市场售价p与上市时间x的关系图是一条折线(如图),写出这种蔬菜的市场售价与时间的函数解析式p=p(x).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
若函数f(x)=x3+x2-2x-2的一个正数零点用二分法计算,附近的函数值参考数据如下:
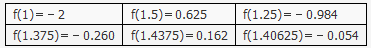
那么方程x3+x2-2x-2=0的一个近似根(精确度0.1)为
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com