
【题目】如图,曲线![]() 与正方形
与正方形![]() :
: ![]() 的边界相切.
的边界相切.
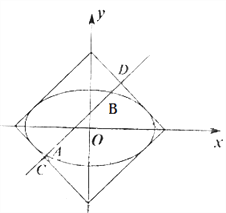
(1)求![]() 的值;
的值;
(2)设直线![]() 交曲线
交曲线![]() 于
于![]() ,交
,交![]() 于
于![]() ,是否存在这样的曲线
,是否存在这样的曲线![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() 成等差数列?若存在,求出实数
成等差数列?若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,再随机抽取3人赠送礼品,记这3人中“微信控”的人数为![]() ,试求
,试求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元.为增加企业竞争力,决定优化产业结构,调整出![]() 名员工从事第三产业,调整后平均每人每年创造利润为
名员工从事第三产业,调整后平均每人每年创造利润为![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线![]() 与正方形
与正方形![]() :
: ![]() 的边界相切.
的边界相切.
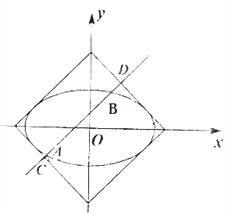
(1)求![]() 的值;
的值;
(2)设直线![]() 交曲线
交曲线![]() 于
于![]() ,交
,交![]() 于
于![]() ,是否存在这样的曲线
,是否存在这样的曲线![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() 成等差数列?若存在,求出实数
成等差数列?若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(Ⅲ)是否存在实数![]() ,对任意
,对任意![]() ,且
,且![]() 有
有![]() 恒成立?
恒成立?
若存在,求出![]() 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,二面角
,二面角![]() 的大小为
的大小为![]() .
.
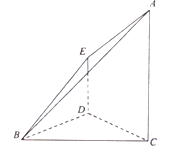
(1)求证: ![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的角(锐角)的大小;
所成的角(锐角)的大小;
(3)若![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com