
(12分)一个多面体的直观图和三视图如图所示,其中M,N分别是AB,AC的中点,G是DF上的一动点.
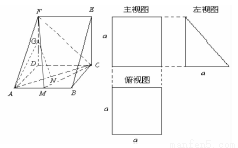
(Ⅰ)求证:GN⊥AC;
(Ⅱ)若点G是DF的中点,求证:GA∥平面FMC.
(I)证明:见解析; (II) 证明:见解析。
【解析】本试题主要考查了三视图和立体几何中的线线垂直和线面平行的综合运用。利用三视图还原几何体,并能理解空间中的线面的位置关系,线线位置关系的运用。
(1)根据由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC,然后利用B、N、D共线,得到线线垂直的证明。
(2)要证明线面平行,先证明面面平行,利用面面平行的性质定理得到结论,关键是得到面GSA // 面FMC
(I)证明:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC……………1分
连接DB,可知B、N、D共线,且AC⊥DN………………3分

又FD⊥AD FD⊥CD,
 FD⊥面ABCD
FD⊥面ABCD
 FD⊥AC ………………5分
FD⊥AC ………………5分
 AC⊥面FDN
AC⊥面FDN 
 GN⊥AC
………………6分
GN⊥AC
………………6分
(II) 证明:取DC中点S,连接AS、GS、GA
 G是DF的中点,
G是DF的中点, GS//FC,AS//CM ………………9分
GS//FC,AS//CM ………………9分
 面GSA // 面FMC………………10分
面GSA // 面FMC………………10分

 GA
// 面FMC
………………12分
GA
// 面FMC
………………12分


科目:高中数学 来源: 题型:
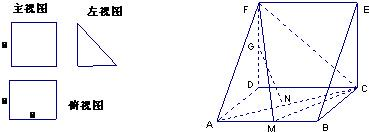 一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.查看答案和解析>>
科目:高中数学 来源: 题型:
| DQ | DP |
查看答案和解析>>
科目:高中数学 来源: 题型:

| |DQ| | |DP| |
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com